题目内容
函数y=Asin(ωx+φ),(A>0,ω>0,|φ|<
)的最小值是-2,在一个周期内图象最高点与最低点横坐标差是3π,又:图象过点(0,1).求
(1)函数解析式;
(2)函数的最大值、以及达到最大值时x的集合.
| π |
| 2 |
(1)函数解析式;
(2)函数的最大值、以及达到最大值时x的集合.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由函数的最值求出A,由周期求出ω,根据特试点的坐标求出φ,可得函数的解析式.
(2)根据正弦函数的图象特征求出函数的最大值、以及达到最大值时x的集合.
(2)根据正弦函数的图象特征求出函数的最大值、以及达到最大值时x的集合.
解答:
解:(1)由题意知:A=2,半周期
=3π=
,求得ω=
,故y=2sin(
x+φ).
再把(0,1)代入,可得2sinφ=1,∴sinφ=
,由,|φ|<
可得 φ=
,故所求函数解析式为y=2sin(
x+
).
(2)令
x+
=2kπ+
,k∈z,求得x=6kπ+π,故当x=6kπ+π 时,函数取得最大值为2,
此时,x的集合为{x|x=6kπ+π,k∈z}.
| T |
| 2 |
| π |
| ω |
| 1 |
| 3 |
| 1 |
| 3 |
再把(0,1)代入,可得2sinφ=1,∴sinφ=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 3 |
| π |
| 6 |
(2)令
| 1 |
| 3 |
| π |
| 6 |
| π |
| 2 |
此时,x的集合为{x|x=6kπ+π,k∈z}.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
椭圆9x2+y2=9的长轴长为( )
| A、2 | B、3 | C、6 | D、9 |
已知集合M={x|-x2+2x>0},N={x|
<1},则M∩N等于( )
| x |
| x-1 |
| A、(0,2) |
| B、(0,1) |
| C、(1,2) |
| D、(-1,1) |
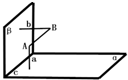 如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.
如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.