题目内容
2.下列命题:①命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
②“x=1”是“x2-3x+2=0”的充分不必要条件
③若p∧q为假命题,则p,q均为假命题
④对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,
说法错误的是③.
分析 写出命题的逆否命题判断①;求解方程,结合充分必要条件的判定方法判断②;由复合命题的真假判断判断③;写出特称命题的否定判断④.
解答 解:①、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”,故①正确;
②、由x2-3x+2=0,解得x=1或x=2,∴“x=1”是“x2-3x+2=0”的充分不必要条件,故②正确;
③、若p∧q为假命题,则p,q中至少有一个为假命题,故③错误;
④、对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,故④正确.
∴错误的命题是③.
故答案为:③.
点评 本题考查命题的真假判断与应用,考查命题的否定与逆否命题,考查充分必要条件的判定方法,是基础题.

练习册系列答案
相关题目
10.已知$\overrightarrow a=(-3,4),\overrightarrow b=(-2,1)$,则$\overrightarrow a$在$\overrightarrow b$上的投影为( )
| A. | -2 | B. | 2 | C. | $-2\sqrt{5}$ | D. | $2\sqrt{5}$ |
9.已知a,b∈R,且ex≥a(x-1)+b对x∈R恒成立,则ab的最大值是( )
| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
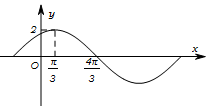 已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.