题目内容
已知f（x）满足f（-x）=-f（x），当x＞0时，其解析式为f（x）=x3+x+1，则当x＜0时，f（x）的解析式为（ ）
| A、f（x）=x3+x-1 |
| B、f（x）=-x3-x-1 |
| C、f（x）=x3-x+1 |
| D、f（x）=-x3-x+1 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据f（x）满足f（-x）=-f（x），转化为当x＞0时，其解析式为f（x）=x3+x+1求解．
解答：
解：∵f（x）满足f（-x）=-f（x），∴f（x）为奇函数，
∵当x＞0时，其解析式为f（x）=x3+x+1，
∴设x＜0，则-x＞0，f（x）=-f（-x）=-[（-x）3+（-x）+1]=x3+x-1，
∴f（x）=x3+x-1，（x＜0）
故选；A
∵当x＞0时，其解析式为f（x）=x3+x+1，
∴设x＜0，则-x＞0，f（x）=-f（-x）=-[（-x）3+（-x）+1]=x3+x-1，
∴f（x）=x3+x-1，（x＜0）
故选；A
点评：本题考查了函数的性质，和求解析式的方法，属于容易题．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知f（x）=
，则y=f（x）的奇偶性是（ ）
| x2+1 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
下列函数中是偶函数的是（ ）
| A、y=x-2 | ||
| B、y=x2，x∈（-2，3] | ||
C、y=-
| ||
| D、y=x3 |
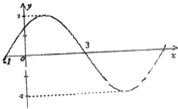已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜