题目内容
18．已知扇形的圆心角为120°，半径为15cm，则扇形的弧长为10π cm（结果保留π）．分析 根据弧长公式即可计算求值．
解答 解：扇形的弧长l=$\frac{nπr}{180}$=$\frac{120•π•15}{180}$=10πcm．
故答案为：10π．
点评 本题主要考查了弧长公式l=$\frac{nπr}{180}$的应用，属于基础题．
练习册系列答案
相关题目
8．
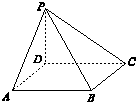如图，在四棱锥P-ABCD中，底面ABCD是边长为m的正方形，PD⊥底面ABCD，且PD=m，PA=PC=$\sqrt{2}$m，若在这个四棱锥内放一个球，则此球的最大半径是（ ）
如图，在四棱锥P-ABCD中，底面ABCD是边长为m的正方形，PD⊥底面ABCD，且PD=m，PA=PC=$\sqrt{2}$m，若在这个四棱锥内放一个球，则此球的最大半径是（ ）| A． | $\frac{1}{3}$（2-$\sqrt{2}$）m | B． | $\frac{1}{2}$（2+$\sqrt{2}$）m | C． | $\frac{1}{2}$（2-$\sqrt{2}$）m | D． | $\frac{1}{6}$（2+$\sqrt{2}$）m |
9．某同学寒假期间对其30位亲属的饮食习惯进行了一次调查，列出了如表2×2列联表：
则可以说其亲属的饮食习惯与年龄有关的把握为（ ）
附：参考公式和临界值表K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| 偏爱蔬菜 | 偏爱肉类 | 合计 | |
| 50岁以下 | 4 | 8 | 12 |
| 50岁以上 | 16 | 2 | 18 |
| 合计 | 20 | 10 | 30 |
附：参考公式和临界值表K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A． | 90% | B． | 95% | C． | 99% | D． | 99.9% |
10．当a=3时，如图的程序框图输出的结果是（ ）
| A． | 9 | B． | 3 | C． | 10 | D． | 6 |
7．过点（3，-2）且与椭圆3x2+8y2=24有相同焦点的椭圆方程为（ ）
| A． | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{10}$=1 | B． | $\frac{{x}^{2}}{10}$+$\frac{{y}^{2}}{15}$=1 | C． | $\frac{{x}^{2}}{15}$+$\frac{{y}^{2}}{10}$=1 | D． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{10}$=1 |