题目内容
13.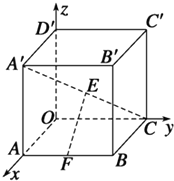 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为$\frac{{\sqrt{2}}}{2}a$.
分析 由在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A(a,0,0),B(a,a,0),C(0,a,0),A′(a,0,a),A′C的中点E与AB的中点F,知F(a,$\frac{a}{2}$,0),E( $\frac{a}{2}$,$\frac{a}{2}$,$\frac{a}{2}$),利用两点间距离公式能求出A′C的中点E与AB的中点F的距离.
解答  解:如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,
解:如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,
∵A(a,0,0),B(a,a,0),C(0,a,0),A′(a,0,a),
A′C的中点E与AB的中点F,
∴F(a,$\frac{a}{2}$,0),E( $\frac{a}{2}$,$\frac{a}{2}$,$\frac{a}{2}$),|EF|=$\sqrt{(a-\frac{a}{2})^{2}+(\frac{a}{2}-\frac{a}{2})^{2}+(0-\frac{a}{2})^{2}}$=$\frac{{\sqrt{2}}}{2}a$.
故答案是:$\frac{{\sqrt{2}}}{2}a$.
点评 本题考查空间中两点间距离公式的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
1.在△ABC中,角A.B、C的对边分别为a,b,c,若2a=3b,则$\frac{9si{n}^{2}B-si{n}^{2}A}{si{n}^{2}A}$=( )
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
8.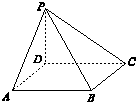 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
 如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )
如图,在四棱锥P-ABCD中,底面ABCD是边长为m的正方形,PD⊥底面ABCD,且PD=m,PA=PC=$\sqrt{2}$m,若在这个四棱锥内放一个球,则此球的最大半径是( )| A. | $\frac{1}{3}$(2-$\sqrt{2}$)m | B. | $\frac{1}{2}$(2+$\sqrt{2}$)m | C. | $\frac{1}{2}$(2-$\sqrt{2}$)m | D. | $\frac{1}{6}$(2+$\sqrt{2}$)m |
5.如果复数z=a+2i满足条件$|z|<\sqrt{5}$,那么实数a的取值范围是( )
| A. | $(-2\sqrt{2},2\sqrt{2})$ | B. | (-2,2) | C. | (-1,1) | D. | $(-\sqrt{3},\sqrt{3})$ |
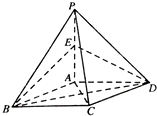 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点,∠BAD=120°.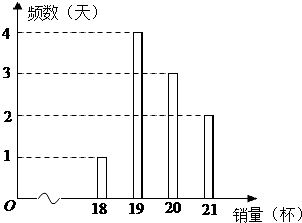 某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示:
某冷饮店只出售一种饮品,该饮品每一杯的成本价为3元,售价为8元,每天售出的第20杯及之后的饮品半价出售.该店统计了近10天的饮品销量,如图所示: