题目内容
3．当x＞1时不等式$\frac{{{x^2}-x+1}}{x-1}≥a$恒成立，则实数a的取值范围是（ ）| A． | （-∞，3] | B． | [3，+∞） | C． | （-∞，2] | D． | [2，+∞） |
分析 化简不等式的左侧，利用基本不等式求出表达式的最小值，然后求出a的范围．
解答 解：当x＞1时，表达式$\frac{{x}^{2}-x+1}{x-1}$=（x-1）+$\frac{1}{x-1}$+1≥2$\sqrt{（x-1）（\frac{1}{x-1}）}$+1=3，当且仅当x=2时取等号．
当x＞1时，不等式$\frac{{{x^2}-x+1}}{x-1}≥a$恒成立，则实数a的取值范围是a≤3．
故选：A．
点评 本题考查函数恒成立，基本不等式的应用，考查分析问题解决问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
12．设A={x|x≥2$\sqrt{2}$}，a=3，下列各式正确的是（ ）
| A． | 0∈A | B． | a∉A | C． | a∈A | D． | {a}∈A |
8．
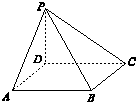如图，在四棱锥P-ABCD中，底面ABCD是边长为m的正方形，PD⊥底面ABCD，且PD=m，PA=PC=$\sqrt{2}$m，若在这个四棱锥内放一个球，则此球的最大半径是（ ）
如图，在四棱锥P-ABCD中，底面ABCD是边长为m的正方形，PD⊥底面ABCD，且PD=m，PA=PC=$\sqrt{2}$m，若在这个四棱锥内放一个球，则此球的最大半径是（ ）| A． | $\frac{1}{3}$（2-$\sqrt{2}$）m | B． | $\frac{1}{2}$（2+$\sqrt{2}$）m | C． | $\frac{1}{2}$（2-$\sqrt{2}$）m | D． | $\frac{1}{6}$（2+$\sqrt{2}$）m |