题目内容
20.下列叙述中正确的是( )| A. | 若a,b,c∈R,则“ax2+bx+c≥0”的充分条件是“b2-4ac≤0” | |
| B. | 若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c” | |
| C. | “直线a∥b”是“直线a⊥平面α,直线b⊥平面α”的必要条件 | |
| D. | b2=ac是a,b,c成等比数列的充要条件 |
分析 A.“b2-4ac≤0”是“ax2+bx+c≥0”既不是充分条件又不是必要条件,与a的取值有关系;
B.“ab2>cb2”推不出“a>c”,b=0时不成立;
C.由“直线a⊥平面α,直线b⊥平面α”利用线面垂直的性质定理可得:a∥b,反之不成立;
D.由a,b,c成等比数列可得:b2=ac,反之不成立,例如a=b=0时.
解答 解:A.a,b,c∈R,则“b2-4ac≤0”是“ax2+bx+c≥0”既不是充分条件又不是必要条件,与a的取值有关系;
B.a,b,c∈R,则“ab2>cb2”推不出“a>c”,b=0时不成立,因此是假命题;
C.由“直线a⊥平面α,直线b⊥平面α”⇒a∥b,反之不成立,因此“直线a∥b”是“直线a⊥平面α,直线b⊥平面α”的必要条件,是真命题;
D.a,b,c成等比数列⇒b2=ac,反之不成立,例如a=b=0时.
故选:C.
点评 本题考查了一元二次方程有实数根与判别式的关系、简易逻辑的判定方法、等比数列的定义、线面垂直的性质定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知双曲线C:$\frac{x^2}{16}-\frac{y^2}{b^2}=1({b>0})$的右焦点与抛物线y2=20x的焦点重合,则双曲线C的渐近线方程为( )
| A. | 4x±3y=0 | B. | 3x±4y=0 | C. | 16x±9y=0 | D. | 9x±16y=0 |
8.已知双曲线的标准方程为$\frac{y^2}{2}-\frac{x^2}{4}$=1,则双曲线的渐近线方程为( )
| A. | y=±2x | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
5.计算机执行下面的程序段后,输出的结果是( )
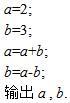
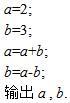
| A. | 5,2 | B. | -1,5 | C. | 5,-1 | D. | 2,5 |
12.若函数f(x)的导函数f′(x)=x(2-x)e-x,则下列关系一定成立的是( )
| A. | f(2)>0 | B. | f(0)>f(1) | C. | f(2)<f(1) | D. | f(2)>f(3) |
9.已知复数z满足|z|=1,则|z+3-4i|(i为虚数单位)的最大值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.已知集合A={1,2,3},集合B={x|x2-6x+8≤0},则A∩B=( )
| A. | {3} | B. | {2,3} | C. | {1,2,3} | D. | [2,3] |