题目内容
17.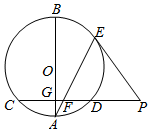 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.(1)求证:PE=PF;
(2)求证:DF•CF=2GF•PF.
分析 (1)利用切线的性质,弦CD垂直于AB,证明∠PEF=∠PFE,即可证明PE=PF;
(2)由△PEF∽△OEB,得出$\frac{PE}{OE}=\frac{EF}{EB}$.△AGF∽△AEB,得出$\frac{AF}{AB}$=$\frac{GF}{EB}$,再将两式相除,把AF•EF=DF•CF,PE=PF,AB=2OE代入即可证明DF•CF=2GF•PF.
解答 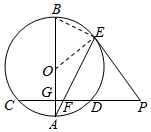 证明:(1)连接OE,则OE⊥EP,∠OAE=∠OEA.
证明:(1)连接OE,则OE⊥EP,∠OAE=∠OEA.
∵弦CD垂直于AB,
∴∠AGF=90°,
∴∠AFG=∠PEF,
∵∠AFG=∠PFE,
∴∠PEF=∠PFE,
∴PE=PF;
(2)连接BE,则
∵△PEF∽△OEB,∴$\frac{PE}{OE}=\frac{EF}{EB}$.①
∵△AGF∽△AEB,∴$\frac{AF}{AB}$=$\frac{GF}{EB}$.②
∵AB=2OE,
∴①÷②可得$\frac{2PE}{AF}$=$\frac{EF}{GF}$,
∴AF•EF=2PE•GF,
∵AF•EF=DF•CF,PE=PF,
∴DF•CF=2GF•PF.
点评 本题考查相似三角形的判定及性质,考查切线的性质,考查学生分析解决问题的能力,有一定难度,关键是对数字2的处理.

练习册系列答案
相关题目
8.已知双曲线的标准方程为$\frac{y^2}{2}-\frac{x^2}{4}$=1,则双曲线的渐近线方程为( )
| A. | y=±2x | B. | $y=±\sqrt{2}x$ | C. | $y=±\frac{1}{2}x$ | D. | $y=±\frac{{\sqrt{2}}}{2}x$ |
5.计算机执行下面的程序段后,输出的结果是( )
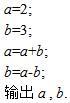
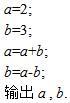
| A. | 5,2 | B. | -1,5 | C. | 5,-1 | D. | 2,5 |
12.若函数f(x)的导函数f′(x)=x(2-x)e-x,则下列关系一定成立的是( )
| A. | f(2)>0 | B. | f(0)>f(1) | C. | f(2)<f(1) | D. | f(2)>f(3) |
9.已知复数z满足|z|=1,则|z+3-4i|(i为虚数单位)的最大值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.在下面给出的四个函数中,既是区间(0,$\frac{π}{2}$)上的增函数,又是以π为周期的偶函数的是( )
| A. | y=|sinx| | B. | y=|cosx| | C. | y=sin2x | D. | y=cos2x |