题目内容
设x，y满足约束条件
，若目标函数z=ax+by（a＞0，b＞0）的最小值为2，则
+
的最小值为（ ）
|
| 3 |
| a |
| 2 |
| b |
| A、12 | B、6 | C、4 | D、2 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用z的几何意义确定取得最小值的条件，然后利用基本不等式进行求则ab的最大值．
解答：
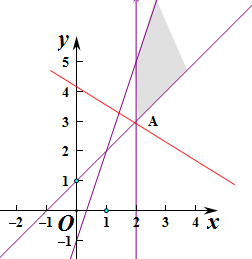解：由z=ax+by（a＞0，b＞0）得y=-
x+
，
∵a＞0，b＞0，
∴直线的斜率-
＜0，
作出不等式对应的平面区域如图：
平移直线得y=-
x+
，由图象可知当直线y=-
x+
经过点A时，直线y=-
x+
的截距最小，此时z最小．
由
，解得
，即A（2，3），
此时目标函数z=ax+by（a＞0，b＞0）的最小值为2，
即2a+3b=2，
则a+
=1，
则
+
=（
+
）（a+
）=3+3+
+
≥6+2
=6+6=12
当且仅当
=
，即3b=2a，即a=
，b=
时取等号．
则
+
的最小值为12，
故选：A
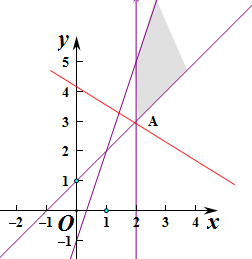解：由z=ax+by（a＞0，b＞0）得y=-| a |
| b |
| z |
| b |
∵a＞0，b＞0，
∴直线的斜率-
| a |
| b |
作出不等式对应的平面区域如图：
平移直线得y=-
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
由
|
|
此时目标函数z=ax+by（a＞0，b＞0）的最小值为2，
即2a+3b=2，
则a+
| 3b |
| 2 |
则
| 3 |
| a |
| 2 |
| b |
| 3 |
| a |
| 2 |
| b |
| 3b |
| 2 |
| 9b |
| 2a |
| 2a |
| b |
|
当且仅当
| 9b |
| 2a |
| 2a |
| b |
| 1 |
| 2 |
| 1 |
| 3 |
则
| 3 |
| a |
| 2 |
| b |
故选：A
点评：本题主要考查线性规划的基本应用，以及基本不等式的应用，利用数形结合求出目标函数取得最大值的条件是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知圆x2+y2+mx-
=0与抛物线y2=4x的准线相切，则m=（ ）
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知p：-2＞-1，q：a-1＜a，则下列判断正确的是（ ）
| A、“p∧q”为假，“￢p”为假 |
| B、“p∧q”为真，“￢p”为真 |
| C、“p∨q”为真，“￢q”为假 |
| D、“p∨q”为假，“￢q”为真 |