题目内容
2．几何体的三视图如图所示，该几何体的体积为（ ）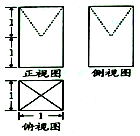
| A． | 2 | B． | $\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | $\frac{5}{3}$ |
分析 由已知中的三视图，可知该几何体是一个长方体，切去了一个边长为1，高也是1的正四棱锥，其体积等于长方体减去正四棱锥的体积．
解答 解：由已知中的三视图，可知该几何体是一个长方体，切去了一个边长为1，高也是1的正四棱锥，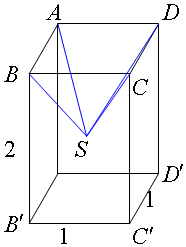
（如图），长方体ABCD-A′B′C′D′切去ABCD-S正四棱锥．
长方体的体积为V长方体=1×1×2=2，
正四棱锥的体积为${V}_{正棱锥}=\frac{1}{3}×1×1×1=\frac{1}{3}$
该几何体的体积$V=2-\frac{1}{3}=\frac{5}{3}$．
故选D
点评 本题考查的知识点是由三视图求体积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
12．若x＞y＞1，0＜a＜b＜1，则下列各式中一定成立的是（ ）
| A． | xa＞yb | B． | xa＜yb | C． | ax＜by | D． | ax＞by |
13．
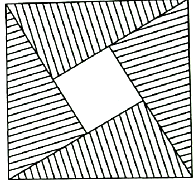如图所示，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形的概率为$\frac{1}{5}$，设直角三角形中较大的锐角为θ，则sinθ=（ ）
如图所示，阴影部分是由四个全等的直角三角形组成的图形，在大正方形内随机取一点，这一点落在小正方形的概率为$\frac{1}{5}$，设直角三角形中较大的锐角为θ，则sinθ=（ ）| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
17．$\frac{1+i}{-2i}$=（ ）
| A． | $-\frac{1}{2}-\frac{1}{2}i$ | B． | $-\frac{1}{2}+\frac{1}{2}i$ | C． | $\frac{1}{2}-\frac{1}{2}i$ | D． | $\frac{1}{2}+\frac{1}{2}i$ |