题目内容
已知函数f(x)=xsinx,x∈[-
,
],则f(
),f(1),f(-
)的大小关系为( )
| π |
| 2 |
| π |
| 2 |
| π |
| 5 |
| π |
| 3 |
A、f(-
| ||||
B、f(1)>f(-
| ||||
C、f(
| ||||
D、f(-
|
考点:函数单调性的性质,利用导数研究函数的单调性
专题:函数的性质及应用
分析:判断函数的奇偶性以及函数的单调性,利用函数的单调性即可得到结论.
解答:
解:∵f(x)=xsinx,
∴f(-x)=-xsin(-x)=xsinx=f(x),
则f(x)是偶函数,当0≤x≤
时,函数y=x是增函数,y=sinx是增函数,
则f(x)=xsinx是增函数,
∴f(-
)=f(
),
∵
>1>
,
∴f(-
)>f(1)>f(
),
故选:A
∴f(-x)=-xsin(-x)=xsinx=f(x),
则f(x)是偶函数,当0≤x≤
| π |
| 2 |
则f(x)=xsinx是增函数,
∴f(-
| π |
| 3 |
| π |
| 3 |
∵
| π |
| 3 |
| π |
| 5 |
∴f(-
| π |
| 3 |
| π |
| 5 |
故选:A
点评:本题主要考查函数值的大小比较,根据函数奇偶性,判断函数单调性的性质是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列结论正确的是( )
| A、若y=cosx,则y′=sinx | ||||
B、若y=sin
| ||||
C、若y=lnx,则y′=
| ||||
| D、若y=2x,则y′=x2x-1 |
如图所示,甲 乙 丙是三个立体图形的三视图,则甲乙丙对应的标号正确的是( )

| A、④③② | B、②①③ |
| C、①②③ | D、③②④ |
在等差数列{an}中,已知ak=1,ak+1=sin2θ,则ak+2=( )
| A、cos2θ |
| B、-cos2θ |
| C、cos2θ |
| D、-cos2θ |
已知数列{an},a1=1,a2=4,且an+2=an+1-an,则数列的第6项为( )
| A、-1 | B、-3 | C、3 | D、-4 |
双曲线
-
=1与
-
=k始终有相同的( )
| x2 |
| 5 |
| y2 |
| 4 |
| x2 |
| 5 |
| y2 |
| 4 |
| A、焦点 | B、准线 |
| C、渐近线 | D、离心率 |
定义A㊣B、B㊣C、C㊣D、D㊣A的运算分别对应图中的(1)、(2)、(3)、(4).则图中的甲、乙的运算式可以表示为:( )
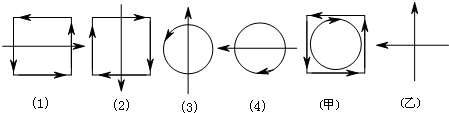

| A、B㊣D、C㊣A |
| B、B㊣D、A㊣C |
| C、D㊣B、C㊣A |
| D、D㊣B、A㊣C |