题目内容
圆A：（x-1）2+（y-1）2=4，圆B：（x-2）2+（y-2）2=9，圆A和圆B的公切线有（ ）
| A、4条 | B、3条 | C、2条 | D、1条 |
考点：圆的切线方程
专题：计算题,直线与圆
分析：求出两个圆的圆心与半径，判断两个圆的位置关系，然后判断公切线的条数．
解答：
解：因为圆A：（x-1）2+（y-1）2=4，它的圆心坐标（1，1），半径为2；
圆B：（x-2）2+（y-2）2=9，它的圆心坐标（2，2），半径为3；
因为圆心距为
，3-2＜
＜3+2，
所以两个圆相交，
所以两个圆的公切线有2条．
故选C．
圆B：（x-2）2+（y-2）2=9，它的圆心坐标（2，2），半径为3；
因为圆心距为
| 2 |
| 2 |
所以两个圆相交，
所以两个圆的公切线有2条．
故选C．
点评：本题考查两个圆的位置关系，直线与圆的位置关系的应用，考查计算能力．
练习册系列答案
相关题目
已知二次函数f（x）=ax2+bx+c，不等式f（x）＞-2x的解集为{x|1＜x＜3}．
（Ⅰ）若方程f（x）=2a有两个相等正根，求f（x）的解析式；
（Ⅱ）若f（x）的最大值为正数，求a的取值范围．
（Ⅰ）若方程f（x）=2a有两个相等正根，求f（x）的解析式；
（Ⅱ）若f（x）的最大值为正数，求a的取值范围．
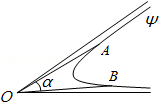如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：f（x）=
|
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数中是偶函数且在（0，+∞）上单调递增的是（ ）
| A、y=2-x |
| B、y=lnx |
| C、y=x-2 |
| D、y=|x|-1 |
已知圆C：x2+（y-3）2=9，过原点作圆C的弦OP，则OP的中点Q的轨迹方程为（ ）
A、（x-
| ||||
B、（x-
| ||||
C、x2+（y-
| ||||
D、x2+（y-
|