Question

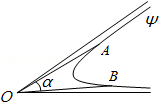如图，对于曲线Ψ所在平面内的点O，若存在以O为顶点的角α，使得α≥∠AOB对于曲线Ψ上的任意两个不同的点A、B恒成立，则称角α为曲线Ψ的相对于点O的“界角”，并称其中最小的“界角”为曲线Ψ的相对于点O的“确界角”．已知曲线C：f（x）=

3x2 4 +1，x≤0 e x e ，x＞0

（其中e=2.71828…是自然对数的底数），O为坐标原点，则曲线C的相对于点O的“确界角”为（　　）

• A、

  π

  3

• B、

  5π

  12

• C、

  π

  2

• D、

  7π

  12

Answer 1

考点：分段函数的应用

专题：导数的综合应用

分析：画出函数f（x）的图象，过点O作出两条直线与曲线相切；，再由两直线的夹角公式即可得到所求的“确界角”．

解答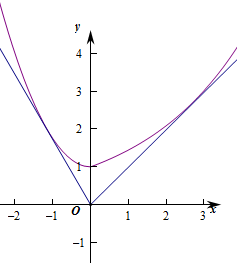： 解：画出函数f（x）的图象，过点O作出两条直线与曲线相切，设它们的方程分别为y=k₁x，y=k₂x，
当x＞0时，y′=f′（x）=

1

e

•e

x

e

，设切点为（m，n），则对应的切线方程为y-

1

e

•e

m

e

=

1

e

•e

m

e

(x-m)，
令x=0，y=0，则-

1

e

•e

m

e

=-

m

e

•e

m

e

，解得m=e，即切线斜率k₁=

1

e

•e

e

e

=

1

e

•e=1，则切线y=k₁x的倾斜角为

π

4

，
当x≤0时，函数的导数f′（x）=

3

2

x，设切点为（a，b），（a＜0）
则切线斜率k=f′（a）=

3a

2

，
则对应的切线方程为y-（

3a2

4

+1）=

3a

2

（x-a），
令a=b=0，则-（

3a2

4

+1）=-

3a

2

•a，
即

3a2

4

=1，则a2=

4

3

，
解得a=-

2 3

3

，
则y=k₂x的斜率k₂=f′（-

2 3

3

）=-

2 3

3

×

3

2

=-

3

，
则切线y=k₂x的倾斜角为

2π

3

，
由两直线的夹角θ=

2π

3

-

π

4

=

5π

12

，
故选：B

点评：本题考查新定义“确界角”及应用，考查导数的应用：求切线，利用导数的几何意义是解决本题的关键．．