题目内容
集合A={x|y=x,x∈R},B={y|y=x2,x∈R},则A∪B= .
考点:并集及其运算
专题:集合
分析:集合A为函数y=x,x∈R的定义域,而集合B为函数y=x2,x∈R的值域,故y≥0,再利用集合并集的含义求解即可.
解答:
解:集A={x|y=x,x∈R}={x|x∈R}=R,B={y|y=x2,x∈R }={y|y≥0},
∴A∪B=R
故答案为:R
∴A∪B=R
故答案为:R
点评:本题考查集合的意义、集合的表示及简单的集合运算,注意描述法表示的集合中代表元素的含义.

练习册系列答案
相关题目
设函数f(x)=x2sinx,则函数f(x)的图象可能为( )
A、 |
B、 |
C、 |
D、 |
若复数z满足z•(1-i)=2-i(其中i是虚数单位),则z=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、“a>b”是“a2>b2”的充分不必要条件 |
| B、命题“?x0∈R,x02+1<0”的否定是:“?x∈R,x2+1>0” |
| C、关于x的方程x2+(a+1)x+a-2=0的两根异号的充要条件是a<1 |
| D、若f(x)为R上的偶函数,则f(x-1)的图象关于直线x=1对称 |
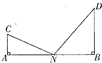 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为