题目内容
已知数列{log2(an+1)}为等差数列,且a1=3,a2=7(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:
+
+…+
<
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
| 1 |
| 2 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列的定义求出数列的公差,即可求数列{an}的通项公式;
(Ⅱ)求出
的表达式,利用等比数列的前n项和公式即可证明不等式.
(Ⅱ)求出
| 1 |
| an+1-an |
解答:
解:(Ⅰ)设等差数列的公差为d,由a1=3,a2=7,
得log2(3+1)=log24=2,log2(7+1)=log28=3,
则d=3-2=1.
所以log2(an+1)=2+(n-1)=n+1,
即an+1=2n+1,
则an=2n+1-1.
(Ⅱ)因为
=
=
,
所以
+
+…+
=
+
+
+…+
=
=
(1-
)<
,
即不等式成立.
得log2(3+1)=log24=2,log2(7+1)=log28=3,
则d=3-2=1.
所以log2(an+1)=2+(n-1)=n+1,
即an+1=2n+1,
则an=2n+1-1.
(Ⅱ)因为
| 1 |
| an+1-an |
| 1 |
| 2n+2-2n+1 |
| 1 |
| 2n+1 |
所以
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| ||||
1-
|
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 2 |
即不等式成立.
点评:本题主要考查等差数列的性质以及等比数列的前n项和公式的应用,考查学生的计算能力.

练习册系列答案
相关题目
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 10 |
| a |
| b |
| 6 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
设函数f(x)=x2sinx,则函数f(x)的图象可能为( )
A、 |
B、 |
C、 |
D、 |
若复数z满足z•(1-i)=2-i(其中i是虚数单位),则z=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD.∠BAD=90°,且PA=AB=BC=1,AD=2,PA⊥平面ABCD,E为AB的中点.
已知四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD.∠BAD=90°,且PA=AB=BC=1,AD=2,PA⊥平面ABCD,E为AB的中点.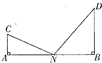 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为