题目内容
若一项数为偶数2m的等比数列的中间两项正好是方程x2+px+q=0的两个根，则此数列的各项积是（ ）
| A、pm |
| B、p2m |
| C、qm |
| D、q2m |
考点：等比数列的前n项和,等比数列的通项公式
专题：等差数列与等比数列
分析：由题意结合韦达定理可得amam+1=q，再由等比数列的性质可得．
解答：
解：由题意记该等比数列为{an}，
则由题意结合韦达定理可得amam+1=q，
∴数列的各项积为（amam+1）m=qm
故选：C
则由题意结合韦达定理可得amam+1=q，
∴数列的各项积为（amam+1）m=qm
故选：C
点评：本题考查等比数列的性质，涉及韦达定理的应用，属基础题．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
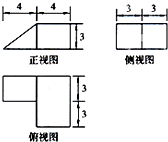
如图所示是一个几何体的三视图，其中正视图是一个正三角形，则这个几何体的表面积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题p：?x∈N，x3＜x2；命题q：?a∈（0，1）∪（1，+∞），函数f（x）=loga（x-1）的图象过点（2，0），则（ ）
| A、p假q真 | B、p真q假 |
| C、p假q假 | D、p真q真 |
已知直线ax+by-
=0（a＞l，b＞1）被圆x2+y2-2x-2y-2=0截得的弦长为2
，则ab的最小值为（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、3-2
| ||
D、3+2
|
已知a=log32，b=log2
，则有（ ）
| 2 |
| 5 |
| A、a=b | B、a＜b |
| C、a＞b | D、a≥b |
已知集合M={2，m}，N={1，2，3}，则“m=3”是“M⊆N”的（ ）
| A、充分而不必条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
“a=1”是“直线ax+（2-a）y+3=0与x-ay-2=0垂直”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |