题目内容
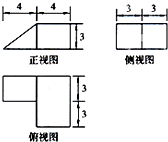
某几何体的三视图(单位:cm)如题所示,则此几何体的体积为 cm3

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个三棱柱和四棱柱的组合体,分别求出它们的体积,累加可得答案.
解答:
解:由已知的三视图可得:该几何体是一个三棱柱和四棱柱的组合体,
三棱柱的底面面积S=
×3×4=6cm2,高为3cm,故体积为18cm3,
四棱锥的底面面积为3×4=12cm2,高为6cm,故体积为72cm3,
故组合体的体积为90cm3,
故答案为:90.
三棱柱的底面面积S=
| 1 |
| 2 |
四棱锥的底面面积为3×4=12cm2,高为6cm,故体积为72cm3,
故组合体的体积为90cm3,
故答案为:90.
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
已知A,B是以O为圆心的单位圆上的动点,且|
|=
,则
•
=( )
| AB |
| 2 |
| OB |
| AB |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
sin
cos
tan
的值为( )
| 7π |
| 6 |
| 2π |
| 3 |
| 5π |
| 4 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知x,y满足
,且目标函数z=2x+y的最小值为1,则实数a的值是( )
|
| A、1 | ||
B、
| ||
C、
| ||
D、
|
若一项数为偶数2m的等比数列的中间两项正好是方程x2+px+q=0的两个根,则此数列的各项积是( )
| A、pm |
| B、p2m |
| C、qm |
| D、q2m |
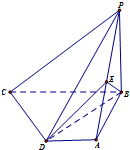 在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°
在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°