题目内容
下列命题中真命题为 .
(1)命题“?x>0,x2-x≤0”的否定是“?x≤0,x2-x>0”
(2)在三角形ABC中,A>B,则sinA>sinB.
(3)已知数列{an},则“an,an+1,an+2成等比数列”是“an+12=an•an+2”的充要条件
(4)已知函数f(x)=lgx+
,则函数f(x)的最小值为2.
(1)命题“?x>0,x2-x≤0”的否定是“?x≤0,x2-x>0”
(2)在三角形ABC中,A>B,则sinA>sinB.
(3)已知数列{an},则“an,an+1,an+2成等比数列”是“an+12=an•an+2”的充要条件
(4)已知函数f(x)=lgx+
| 1 |
| lgx |
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1),写出命题“?x>0,x2-x≤0”的否定,可判断(1);
(2),在三角形ABC中,利用大角对大边及正弦定理可判断(2);
(3),利用充分必要条件的概念可分析判断(3);
(4),f(x)=lgx+
,分x>1与0<x<1两种情况讨论,利用对数函数的单调性质可判断(4).
(2),在三角形ABC中,利用大角对大边及正弦定理可判断(2);
(3),利用充分必要条件的概念可分析判断(3);
(4),f(x)=lgx+
| 1 |
| lgx |
解答:
解:对于(1),命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0”,故(1)错误;
对于(2),在三角形ABC中,A>B?a>b?sinA>sinB,故(2)正确;
对于(3),数列{an}中,若an,an+1,an+2成等比数列,则an+12=an•an+2,即充分性成立;反之,若an+12=an•an+2,则数列{an}不一定是等比数列,如an=0,满足an+12=an•an+2,但该数列不是等比数列,即必要性不成立,故(3)错误;
对于(4),函数f(x)=lgx+
,则当x>1时,函数f(x)的最小值为2,当0<x<1时,f(x)=lgx+
<0,故(4)错误.
综上所述,只有(2)正确,
故答案为:(2).
对于(2),在三角形ABC中,A>B?a>b?sinA>sinB,故(2)正确;
对于(3),数列{an}中,若an,an+1,an+2成等比数列,则an+12=an•an+2,即充分性成立;反之,若an+12=an•an+2,则数列{an}不一定是等比数列,如an=0,满足an+12=an•an+2,但该数列不是等比数列,即必要性不成立,故(3)错误;
对于(4),函数f(x)=lgx+
| 1 |
| lgx |
| 1 |
| lgx |
综上所述,只有(2)正确,
故答案为:(2).
点评:本题考查命题的真假判断与应用,综合考查命题的否定、正弦定理的应用及等比数列的性质、充分必要条件的概念及应用,考查对数函数的性质,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a、b、c,若a•cosA=bcosB,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
 如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=
如图,四边形ABCD是正方形,PD∥MA,MA⊥AD,PM⊥平面CDM,MA=AD=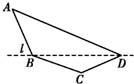 某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).
某单位设计一个展览沙盘,现欲在沙盘平面内,铺设一个对角线在L上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,使A+C=180°,且AB=BC.设AB=x米,cos A=f(x).