题目内容
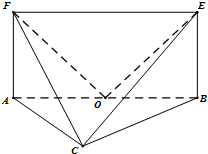 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.(Ⅰ)求证:OE⊥FC;
(Ⅱ)求二面角E-FC-O的正切值.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明OE⊥FC,只需证明OE⊥平面OFC,只需证明OF⊥OE,OC⊥OE;
(Ⅱ)过O作OG⊥FC,垂足为G,连接EG,则∠OGE就是二面角E-FC-O的平面角,求出OG,OE,即可求二面角E-FC-O的正切值.
(Ⅱ)过O作OG⊥FC,垂足为G,连接EG,则∠OGE就是二面角E-FC-O的平面角,求出OG,OE,即可求二面角E-FC-O的正切值.
解答:
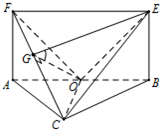 (Ⅰ)证明:连结OC,因AC=BC,O是AB的中点,
(Ⅰ)证明:连结OC,因AC=BC,O是AB的中点,
故OC⊥AB. …(1分)
又因平面ABC⊥平面ABEF,
故OC⊥平面ABEF,
于是OC⊥OF. …(3分)
又OF⊥EC,
所以OF⊥平面OEC,
所以OF⊥OE,…(5分)
又因OC⊥OE,故OE⊥平面OFC,
所以OE⊥FC. …(7分)
(Ⅱ)解:由(Ⅰ),得AB=2AF.不妨设AF=1,则AB=2.
因为△ABC为等边三角形,则AC=BC=2,…(9分)
过O作OG⊥FC,垂足为G,连接EG,
则∠OGE就是二面角E-FC-O的平面角.…(11分)
在△OFC中,FC=
,CO=
,OF=
,
所以
OG=
•
,
所以OG=
,
又EO=
,
所以tan∠EGO=
=
,
即二面角E-FC-O的正切值为
. …(14分)
 (Ⅰ)证明:连结OC,因AC=BC,O是AB的中点,
(Ⅰ)证明:连结OC,因AC=BC,O是AB的中点,故OC⊥AB. …(1分)
又因平面ABC⊥平面ABEF,
故OC⊥平面ABEF,
于是OC⊥OF. …(3分)
又OF⊥EC,
所以OF⊥平面OEC,
所以OF⊥OE,…(5分)
又因OC⊥OE,故OE⊥平面OFC,
所以OE⊥FC. …(7分)
(Ⅱ)解:由(Ⅰ),得AB=2AF.不妨设AF=1,则AB=2.
因为△ABC为等边三角形,则AC=BC=2,…(9分)
过O作OG⊥FC,垂足为G,连接EG,
则∠OGE就是二面角E-FC-O的平面角.…(11分)
在△OFC中,FC=
| 5 |
| 3 |
| 2 |
所以
| 5 |
| 3 |
| 2 |
所以OG=
| ||
|
又EO=
| 2 |
所以tan∠EGO=
| EO |
| EG |
| ||
| 3 |
即二面角E-FC-O的正切值为
| ||
| 3 |
点评:本题考查线面垂直的判定与性质,考查面面角,考查学生分析解决问题的能力,正确作出面面角是关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
已知△ABC中,a=2,sinA:sinB=
:3,则边b=( )
| 3 |
A、
| ||
B、2
| ||
C、3
| ||
| D、3 |
各项均为正数的等比数列{an}中,2a1+a2=a3,则
的值为( )
| a4+a5 |
| a3+a4 |
| A、-1 | B、-1或2 | C、3 | D、2 |
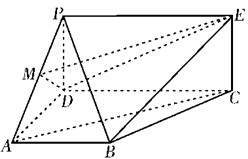 如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=
如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=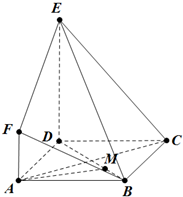 如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.
如图,ABCD是边长为2的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF=3.
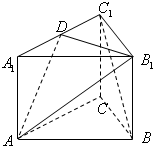 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为