题目内容
已知数列{an}为等比数列,前n项和为Sn,求证:Sn2+S2n2=Sn(S2n+S3n).
考点:数列的求和
专题:等差数列与等比数列
分析:根据等比数列性质,有S2n=Sn+qnSn=Sn(1+qn),S3n=Sn+qnSn+q2nSn.由此能证明Sn2+S2n2=Sn(S2n+S3n).
解答:
证明:根据等比数列性质,有
S2n=Sn+qnSn=Sn(1+qn),
S3n=Sn+qnSn+q2nSn.
∴Sn2+S2n2=Sn2+[Sn(1+qn)2
=Sn2(2+2qn+q2n).
Sn(S2n+S3n)=Sn2(2+2qn+q2n).
∴Sn2+S2n2=Sn(S2n+S3n).
S2n=Sn+qnSn=Sn(1+qn),
S3n=Sn+qnSn+q2nSn.
∴Sn2+S2n2=Sn2+[Sn(1+qn)2
=Sn2(2+2qn+q2n).
Sn(S2n+S3n)=Sn2(2+2qn+q2n).
∴Sn2+S2n2=Sn(S2n+S3n).
点评:本题考查关于等比数列的前n项和的证明,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、18π | ||
| D、20π |
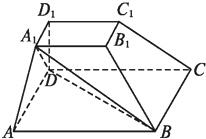 如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2A1B1=2AD=2DD1,∠BAD=60°. 如图,已知点D、E分别是三棱柱ABC-A1B1C1的棱BC、A1B1的中点.求证:VE-ABD=2VE-DC
如图,已知点D、E分别是三棱柱ABC-A1B1C1的棱BC、A1B1的中点.求证:VE-ABD=2VE-DC