题目内容
已知Ω={(x,y)|x+y<6,x>0,y>0},A={(x,y)|0<x<4,y>0,x-4y+4>0},若向区域Ω上随机投掷一点P,则点P落入区域A中的概率为 .
考点:几何概型
专题:概率与统计
分析:作出不等式组对应的平面区域,求出对应区域的面积,利用几何概型的概率公式即可得到结论.
解答:
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
则区域Ω是面积为S=
×6×6=18,
区域A对应的区域为矩形OECD,则D(0,1),E(4,0),C(4,2),
对应的面积S′=
=6,
根据几何概型的概率公式可得若向区域Ω上随机投掷一点P,则点P落入区域A中的概率为:
=
,
故答案为:
.
 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:则区域Ω是面积为S=
| 1 |
| 2 |
区域A对应的区域为矩形OECD,则D(0,1),E(4,0),C(4,2),
对应的面积S′=
| (1+2)×4 |
| 2 |
根据几何概型的概率公式可得若向区域Ω上随机投掷一点P,则点P落入区域A中的概率为:
| 6 |
| 18 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题主要考查几何概型的计算,利用不等式组表示平面区域,求出对应的面积是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知a=2ln3,b=2lg2,c=(
) log
,则( )
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、c>a>b |
| B、a>b>c |
| C、a>c>b |
| D、b>c>a |
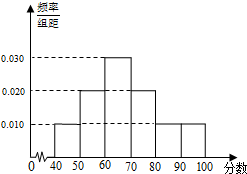 某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是
某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计,得到如图所示的样本频率分布直方图.若规定60分及以上为合格,则估计这1000名学生中合格人数是