题目内容
(x-
)6的二项展开式中含x3的项的系数为 .
| 1 | ||
|
考点:二项式系数的性质
专题:计算题,二项式定理
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为3求出展开式中含x3项的系数.
解答:
解:(x-
)6的展开式的通项为Tr+1=C6r(-1)rx6-
,
令6-
r=3得r=2
故展开式中含x3项的系数是C62×(-1)2=15.
故答案为:15.
| 1 | ||
|
| 3r |
| 2 |
令6-
| 3r |
| 2 |
故展开式中含x3项的系数是C62×(-1)2=15.
故答案为:15.
点评:二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目
若圆锥的轴截面是等边三角形,则它的侧面展开图扇形的圆心角为( )
| A、90° | B、180° |
| C、45° | D、60° |
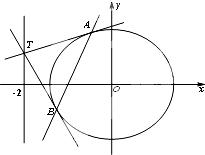 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q.动点M满足
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q.动点M满足