题目内容
已知z为复数,|z|=1,则|z2-3|的最大值是 .
考点:复数求模
专题:数系的扩充和复数
分析:意义|z|=1,可设z=cosθ+isinθ,θ∈[0,2π).利用模的计算公式可得|z2-3|=|cos2θ-sin2θ-3+isin2θ|=
,再利用三角函数的单调性即可得出.
| (cos2θ-3)2+sin22θ |
解答:
解:∵|z|=1,∴可设z=cosθ+isinθ,θ∈[0,2π).
∴|z2-3|=|cos2θ-sin2θ-3+isin2θ|=
=
≤
=4,
当cos2θ=-1时,取等号.
∴|z2-3|的最大值是4.
故答案为:4.
∴|z2-3|=|cos2θ-sin2θ-3+isin2θ|=
| (cos2θ-3)2+sin22θ |
| 10-6cos2θ |
| 10-6×(-1) |
当cos2θ=-1时,取等号.
∴|z2-3|的最大值是4.
故答案为:4.
点评:本题考查了复数的运算法则、模的计算公式、三角函数的单调性,属于基础题.

练习册系列答案
相关题目
 如图是一个封闭几何体的三视图,则该几何体的表面积为( )
如图是一个封闭几何体的三视图,则该几何体的表面积为( )| A、7πcm2 |
| B、8πcm2 |
| C、9πcm2 |
| D、11πcm2 |
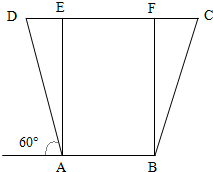 如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°,
如图,水渠的横截面积是等腰梯形,下底及两边坡的总长度为a,坡AD的倾角为60°, 样本容量为100的频率分布直方图如图所示,由此估计样本数据落在[6,10]内的频数为
样本容量为100的频率分布直方图如图所示,由此估计样本数据落在[6,10]内的频数为