题目内容
9.欧拉公式eix=cosx+isinx (i为虚数单位)是瑞士数学家欧拉发明的,将指数的定义域扩大到复数集,建立了三角函数和指数函数的联系,被誉为“数学中的天桥”.根据欧拉公式可知,e${\;}^{\frac{π}{3}i}$表示的复数的模为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{3}$ |
分析 直接由题意可得${e}^{\frac{π}{3}i}$=cos$\frac{π}{3}$+isin$\frac{π}{3}$,再由复数模的计算公式得答案.
解答 解:由题意,${e}^{\frac{π}{3}i}$=cos$\frac{π}{3}$+isin$\frac{π}{3}$,
∴e${\;}^{\frac{π}{3}i}$表示的复数的模为$\sqrt{co{s}^{2}\frac{π}{3}+si{n}^{2}\frac{π}{3}}=1$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
20.己知复数z=$\frac{a+3i}{1+2i}$(a∈R,i是虚数单位)是纯虚数,则|z|为( )
| A. | $\frac{3}{2}$ | B. | $\frac{15}{2}$ | C. | 6 | D. | 3 |
17.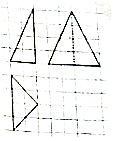 一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
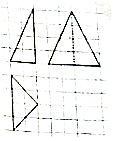 一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )| A. | 16π | B. | 32π | C. | 48π | D. | 64π |
4.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点F(c,0)作圆x2+y2=a2的切线,切点为M.直线FM交抛物线y2=-4cx于点N,若$\overrightarrow{OF}+\overrightarrow{ON}=2\overrightarrow{OM}$(O为坐标原点),则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\sqrt{5}$ | D. | $1+\sqrt{5}$ |
14.若数列{an}是正项数列,且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=n2+n,则a1+$\frac{{a}_{2}}{2}$+…+$\frac{{a}_{n}}{n}$等于( )
| A. | 2n2+2n | B. | n2+2n | C. | 2n2+n | D. | 2(n2+2n) |
1.若△ABC的内角A,B,C所对的边分别为a,b,c,已知2bsin2A=3asinB,且c=2b,则$\frac{a}{b}$等于( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
6.已知f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{{x}^{2}-ax,x≥0}\end{array}\right.$,且g(x)=f(x)+$\frac{x}{2}$有三个零点,则实数a的取值范围为( )
| A. | ($\frac{1}{2}$,+∞) | B. | [1,+∞) | C. | (0,$\frac{1}{2}$ ) | D. | (0,1] |