题目内容
8.在数列{an}中,若$\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+$\sqrt{2}$,a1=8,则数列{an}的通项公式为( )| A. | an=2(n+1)2 | B. | an=4(n+1) | C. | an=8n2 | D. | an=4n(n+1) |
分析 $\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+$\sqrt{2}$,a1=8,则数列{$\sqrt{{a}_{n}}$}为等差数列.利用通项公式即可得出.
解答 解:∵$\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+$\sqrt{2}$,a1=8,则数列{$\sqrt{{a}_{n}}$}为等差数列.
∴$\sqrt{{a}_{n}}$=$\sqrt{8}$+(n-1)$\sqrt{2}$=$\sqrt{2}$(n+1).
∴an=2(n+1)2.
故选:A.
点评 本题考查了等差数列的通项公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
3.定义在(0,+∞)上的函数f(x)满足f(x)>2(x+$\sqrt{x}$)f′(x),其中f′(x)为f(x)的导函数,则下列不等式中,一定成立的是( )
| A. | f(1)>$\frac{f(2)}{2}$>$\frac{f(3)}{3}$ | B. | $\frac{f(1)}{2}$>$\frac{f(4)}{3}$>$\frac{f(9)}{4}$ | C. | f(1)<$\frac{f(2)}{2}$<$\frac{f(3)}{3}$ | D. | $\frac{f(1)}{2}$<$\frac{f(4)}{3}$<$\frac{f(9)}{4}$ |
20.己知复数z=$\frac{a+3i}{1+2i}$(a∈R,i是虚数单位)是纯虚数,则|z|为( )
| A. | $\frac{3}{2}$ | B. | $\frac{15}{2}$ | C. | 6 | D. | 3 |
17.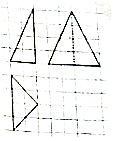 一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
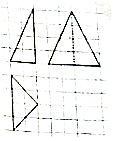 一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )
一个三棱锥的三视图如图(图中小正方形的边长为1),若这个三角棱锥的顶点都在同一个球的球面上,则这个球的表面积是( )| A. | 16π | B. | 32π | C. | 48π | D. | 64π |
6.已知f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{{x}^{2}-ax,x≥0}\end{array}\right.$,且g(x)=f(x)+$\frac{x}{2}$有三个零点,则实数a的取值范围为( )
| A. | ($\frac{1}{2}$,+∞) | B. | [1,+∞) | C. | (0,$\frac{1}{2}$ ) | D. | (0,1] |