题目内容
已知f(x)=x2-px+q,其中p>0,q>0.
(Ⅰ)当p>q时,证明
<
;
(Ⅱ)若f(x)=0在区间(0,1],(1,2]内各有一个根,求p+q的取值范围;
(Ⅲ)设数列{an}的首项a1=1,前n项和Sn=f(n),n∈N*,求an,并判断{an}是否为等差数列?
(Ⅰ)当p>q时,证明
| f(q) |
| p |
| f(p) |
| q |
(Ⅱ)若f(x)=0在区间(0,1],(1,2]内各有一个根,求p+q的取值范围;
(Ⅲ)设数列{an}的首项a1=1,前n项和Sn=f(n),n∈N*,求an,并判断{an}是否为等差数列?
考点:一元二次方程的根的分布与系数的关系,二次函数的性质,等差数列的性质
专题:函数的性质及应用
分析:(Ⅰ)当p>q时,分别化简
、
,再把它们作差判断符号,即可证得结论.
(Ⅱ)由题意可得
,求得
,画出点(p,q)(p>0,q>0)组成的可行域,由线性规划知识求得p+q的范围.
(Ⅲ)根据数列{an}的前n项和Sn=f(n)与第n项an的关系,求出数列的前两项以及an+1-an的值,判断数列{an}是否为等差数列.
| f(p) |
| q |
| f(q) |
| p |
(Ⅱ)由题意可得
|
|
(Ⅲ)根据数列{an}的前n项和Sn=f(n)与第n项an的关系,求出数列的前两项以及an+1-an的值,判断数列{an}是否为等差数列.
解答:
解:(Ⅰ)∵
=
=
-q,
=
=1,
∴
-
=
-q-1=
.
∵p>q>0,∴
<0,即
-
<0,∴
<
.
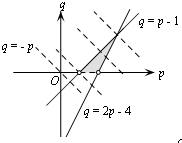
(Ⅱ)∵抛物线的图象开口向上,且f(x)=0在区间(0,1],(1,2]内各有一个根,
∴
⇒
⇒
,∴点(p,q)(p>0,q>0)组成的可行域如图所示,
设z=p+q,由线性规划知识可知,1<z=p+q≤5,即p+q∈(1,5].
(Ⅲ)设数列{an}的首项a1=1,前n项和Sn=f(n)=n2-pn+q,n∈N*,
当n=1时,a1=s1=1-p+q=1,∴p=q.
当n≥2时,an=Sn-Sn-1=(n2-pn+q)-[(n-1)2-p(n-1)+q]=2n-p-1.
∴an=
.
再根据 a1=1,a2=3-p,an+1-an=2 (n≥2),p>0,q>0,
可得{an}不是等差数列.
| f(q) |
| p |
| q2-pq+q |
| p |
| q2+q |
| p |
| f(p) |
| q |
| p2-p2+q |
| q |
∴
| f(q) |
| p |
| f(p) |
| q |
| q2+q |
| p |
| (q+1)(q-p) |
| p |
∵p>q>0,∴
| (q+1)(q-p) |
| p |
| f(q) |
| p |
| f(p) |
| q |
| f(q) |
| p |
| f(p) |
| q |
(Ⅱ)∵抛物线的图象开口向上,且f(x)=0在区间(0,1],(1,2]内各有一个根,
∴
|
|
|
设z=p+q,由线性规划知识可知,1<z=p+q≤5,即p+q∈(1,5].

(Ⅲ)设数列{an}的首项a1=1,前n项和Sn=f(n)=n2-pn+q,n∈N*,
当n=1时,a1=s1=1-p+q=1,∴p=q.
当n≥2时,an=Sn-Sn-1=(n2-pn+q)-[(n-1)2-p(n-1)+q]=2n-p-1.
∴an=
|
再根据 a1=1,a2=3-p,an+1-an=2 (n≥2),p>0,q>0,
可得{an}不是等差数列.
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,等产数列的定义和性质,体现了数形结合、分类讨论、转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目