题目内容
已知集合，A={x|x＜a+1}．B={x|x＞-1}．
（1）若a=1，求A∩B；
（2）若A∪B=R，求实数a的取值范围．
（1）若a=1，求A∩B；
（2）若A∪B=R，求实数a的取值范围．
考点：交集及其运算
专题：集合
分析：（1）将a=1代入A中不等式确定出A，求出A与B的交集即可；
（2）根据A与B的并集为R，列出关于a的不等式，求出不等式的解集即可确定出a的范围．
（2）根据A与B的并集为R，列出关于a的不等式，求出不等式的解集即可确定出a的范围．
解答：
解：（1）将a=1代入A中不等式得：x＜2，即A={x|x＜2}，
∵B={x|x＞-1}，
∴A∩B={x|-1＜x＜2}；
（2）∵A={x|x＜a+1}，B={x|x＞-1}，且A∪B=R，
∴a+1＞-1，
解得：a＞-2．
∵B={x|x＞-1}，
∴A∩B={x|-1＜x＜2}；
（2）∵A={x|x＜a+1}，B={x|x＞-1}，且A∪B=R，
∴a+1＞-1，
解得：a＞-2．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
设二次函数f（x）=ax2-4x+c（x∈R）的值域为[0，+∞），
+
则的最大值是（ ）
| 1 |
| c+1 |
| 9 |
| a+9 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
条件p：|x+1|＞2，条件q：
＜0，则?p是?q的（ ）
| 1 |
| 4+x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
执行如图所示的算法程序，则输出结果为（ ）
| A、2 | B、6 | C、42 | D、1806 |
设数列{an}中，a1=2，an+1=an+n+1，数列{bn}满足bn=
（n∈N*），则数列{bn}的前n项和为（ ）
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
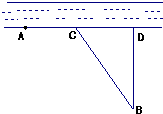在甲、乙两个工厂，甲厂位于一直线河岸的岸边A处，乙厂与甲厂在河的同侧，乙厂位于离河岸40km的B处，乙厂到河岸的垂足D与A相距50km，两厂要在他们之间的此岸边合建一个污水处理厂C，从污水处理厂到甲厂和乙厂的铺设的排污管道费用分别为每千米3a元和5a元，记铺设管道的总费用为y元．