题目内容
已知
=（2，1），
=（sinx，cosx），且
∥
．
求值：（1）tanx
（2）
．
| a |
| b |
| a |
| b |
求值：（1）tanx
（2）
| 3sinx-cosx |
| sinx+3cosx |
考点：同角三角函数基本关系的运用,平面向量共线（平行）的坐标表示
专题：三角函数的求值
分析：（1）由两向量平行时满足的关系，根据两向量坐标列出关系式，整理即可求出tanx的值；
（2）原式分子分母除以cosx变形后，将tanx的值代入计算即可求出值．
（2）原式分子分母除以cosx变形后，将tanx的值代入计算即可求出值．
解答：
解：（1）∵
=（2，1），
=（sinx，cosx），且
∥
，
∴sinx=2cosx，即tanx=2；
（2）∵tanx=2，
∴原式=
=
=1．
| a |
| b |
| a |
| b |
∴sinx=2cosx，即tanx=2；
（2）∵tanx=2，
∴原式=
| 3tanx-1 |
| 3+tanx |
| 6-1 |
| 3+2 |
点评：此题考查了同角三角函数基本关系的运用，以及平面向量共线（平行）的坐标表示，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
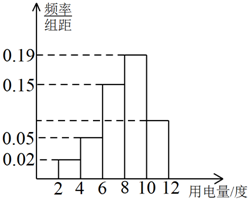为了解某地区用电高峰期居民的用电量，抽取一个容量为200的样本，记录某天各户居民的用电量（单位：度），制成频率分布直方图，如图．