题目内容
已知直线l,m和平面α,β,γ.
①α⊥γ,β⊥γ
②l∥m,l⊥α,m⊥β
③l?α,m?α,l∥β,m∥β
④l和m异面,l?α,m?β,l∥β,m∥α
上面各项条件中能推出α∥β的是 项(把你认为符合条件的序号都填上).
①α⊥γ,β⊥γ
②l∥m,l⊥α,m⊥β
③l?α,m?α,l∥β,m∥β
④l和m异面,l?α,m?β,l∥β,m∥α
上面各项条件中能推出α∥β的是
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:①面面垂直的性质;②线面垂直的性质;③线面平行的判定;④面面平行的判定.
解答:
解:对于①α⊥γ,β⊥γ,α、β有可能平行,也有可能相交,所以不能得出α∥β;
②l∥m,l⊥α,∴m⊥α,又m⊥β,∴α∥β;
③若l∥m,α、β可能相交;
④l和m异面,l?α,在α内作直线n,使得n∥m,l和n必相交,l∥β,n∥β,所以α∥β;
故答案为②④
②l∥m,l⊥α,∴m⊥α,又m⊥β,∴α∥β;
③若l∥m,α、β可能相交;
④l和m异面,l?α,在α内作直线n,使得n∥m,l和n必相交,l∥β,n∥β,所以α∥β;
故答案为②④
点评:本题主要考查线面,面面,平行与垂直的判定及性质.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
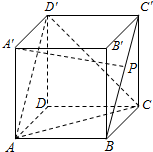 如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题:
如图,点P在正方体ABCD-A′B′C′D′的面对角线BC′上运动.给出下列三个命题: