题目内容
函数y=sin(x+
),x∈[0,2π]的单调减区间是 .
| π |
| 3 |
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:先利用正弦函数的单调性求得函数的单调减区间,进而根据x的范围截取即可.
解答:
解:由2kπ+
≤x+
≤2kπ+
,得2kπ+
≤x≤
+2kπ,k∈Z,
∴函数的单调减区间为[2kπ+
,
+2kπ](k∈Z),
∵x∈[0,2π],
∴函数y的单调减区间为[
,
],
故答案为:[
,
].
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
∴函数的单调减区间为[2kπ+
| π |
| 6 |
| 7π |
| 6 |
∵x∈[0,2π],
∴函数y的单调减区间为[
| π |
| 6 |
| 7π |
| 6 |
故答案为:[
| π |
| 6 |
| 7π |
| 6 |
点评:本题主要考查了三角函数图象与性质.注意运用整体法和数形结合思想来解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在极坐标系中,方程ρ=2cosθ的图形是( )
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
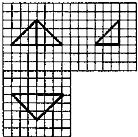 如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为
如图,网格纸上小正方形的边长为2,粗线画出的是某几何体的三视图,则此几何体的体积为