题目内容
求函数y=log
（-x2+4x+5）的定义域和值域．
| 1 |
| 3 |
考点：对数函数的定义域
专题：函数的性质及应用
分析：y=log
（-x2+4x+5）中，由-x2+4x+5＞0，能求出其定义域为；设t=-x2+4x+5=-（x-2）2+9≤9，由y=log
（-x2+4x+5）=log
t≥log
9=-2，能求出其值域．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：
解：y=log
（-x2+4x+5）中，
-x2+4x+5＞0，
解得-1＜x＜5，
∴函数y=log
（-x2+4x+5）的定义域为（-1，5）．
设t=-x2+4x+5=-（x-2）2+9≤9，
∴y=log
（-x2+4x+5）=log
t≥log
9=-2，
∴函数y=log
（-x2+4x+5）的值域为[-2，+∞）．
| 1 |
| 3 |
-x2+4x+5＞0，
解得-1＜x＜5，
∴函数y=log
| 1 |
| 3 |
设t=-x2+4x+5=-（x-2）2+9≤9，
∴y=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴函数y=log
| 1 |
| 3 |
点评：本题考查指数函数的定义域和值域的求法，是基础题，解题时要注意指数函数的性质的合理运用．
练习册系列答案
相关题目
当x∈（0，5）时，函数y=xlnx的单调性（ ）
| A、是单调增函数 | ||||
| B、是单调减函数 | ||||
C、在（0，
| ||||
D、在（0，
|
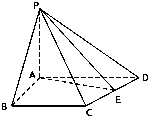在四棱锥P-ABCD中，侧面PAD与侧面PAB都是以A为直角顶点的直角三角形，底面ABCD是直角梯形，AD∥BC，∠ABC=90°，AB=4，BC=3，AD=5，E是CD的中点．