题目内容
已知两条直线l1:mx+8y+n=0和直线l2:2x+my-1=0;求满足下列条件时相应m,n的值:
(1)l1与l2相交于点A(m,-1);
(2)当m>0,l1∥l2,且l1在x轴上的截距为1;
(3)l1⊥l2,且l1在y轴上的截距为-1.
(1)l1与l2相交于点A(m,-1);
(2)当m>0,l1∥l2,且l1在x轴上的截距为1;
(3)l1⊥l2,且l1在y轴上的截距为-1.
考点:直线的一般式方程
专题:直线与圆
分析:(1)将点P(m,-1)代入两直线方程,解出m和n的值.
(2)由 l1∥l2 得斜率相等,求出 m 值,然后由l1在x轴上的截距为1求得n的值.
(3)先检验斜率不存在的情况,当斜率存在时,看斜率之积是否等于1,从而得到结论.
(2)由 l1∥l2 得斜率相等,求出 m 值,然后由l1在x轴上的截距为1求得n的值.
(3)先检验斜率不存在的情况,当斜率存在时,看斜率之积是否等于1,从而得到结论.
解答:
解:两条直线l1:mx+8y+n=0和直线l2:2x+my-1=0.
(1)将点P(m,-1)代入两直线方程得:m2-8+n=0 和 2m-m-1=0,
解得 m=1,n=7.
(2)由 l1∥l2 得:m2-8×2=0,m=±4,
又两直线不能重合,
∴有 8×(-1)-mn≠0,对应得 n≠2m,
又l1在x轴上的截距为1,
∴当m=4,n=-4或m=-4,n=4.
(3)当m=0时,直线l1:y=-
和 l2:x=
,此时,l1⊥l2,
要使l1在y轴上的截距为-1,则n=8.
当m≠0时此时两直线的斜率之积等于
,显然 l1与l2不垂直,
∴当m=0,n=8时直线 l1 和 l2垂直,且l1在y轴上的截距为-1.
(1)将点P(m,-1)代入两直线方程得:m2-8+n=0 和 2m-m-1=0,
解得 m=1,n=7.
(2)由 l1∥l2 得:m2-8×2=0,m=±4,
又两直线不能重合,
∴有 8×(-1)-mn≠0,对应得 n≠2m,
又l1在x轴上的截距为1,
∴当m=4,n=-4或m=-4,n=4.
(3)当m=0时,直线l1:y=-
| n |
| 8 |
| 1 |
| 2 |
要使l1在y轴上的截距为-1,则n=8.
当m≠0时此时两直线的斜率之积等于
| 1 |
| 4 |
∴当m=0,n=8时直线 l1 和 l2垂直,且l1在y轴上的截距为-1.
点评:本题考查两直线平行、垂直的性质,两直线平行,斜率相等,两直线垂直,斜率之积等于-1,注意斜率相等的两直线可能重合,要进行排除,是中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
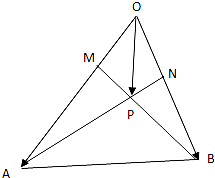 如图,在△OAB中,
如图,在△OAB中,