题目内容
7.求下列各曲线的标准方程(1)长轴长为12,离心率为$\frac{2}{3}$,焦点在x轴上的椭圆;
(2)过点A$(\frac{{\sqrt{6}}}{3},\sqrt{3})$和 B$(\frac{{2\sqrt{2}}}{3},1)$的椭圆的标准方程.
分析 (1)题目明确了要求椭圆的焦点在x轴上,可以设其标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>>0),结合题意可得长轴长2a为12,则a=6,再由离心率公式可得c的值,计算可得b的值,将a、b的值代入椭圆的标准方程可得答案;
(2)根据题意,设设要求椭圆的标准方程为:mx2+ny2=1,(m、n>0),结合题意可得$\left\{\begin{array}{l}{\frac{2}{3}m+3n=1}\\{\frac{8}{9}m+n=1}\end{array}\right.$,解可得m、n的值,将其代入椭圆的方程可得答案.
解答 解:(1)根据题意,要求椭圆的焦点在x轴上,可以设其标准方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>>0),
又由题意,其长轴长为12,即2a=12,则a=6,
其离心率为$\frac{2}{3}$,即e=$\frac{c}{a}$=$\frac{2}{3}$,则c=4,
故b2=a2-c2=20,
故椭圆的标准方程为:$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1;
(2)根据题意,设要求椭圆的标准方程为:mx2+ny2=1,(m、n>0)
椭圆过点A$(\frac{{\sqrt{6}}}{3},\sqrt{3})$和 B$(\frac{{2\sqrt{2}}}{3},1)$,
则有$\left\{\begin{array}{l}{\frac{2}{3}m+3n=1}\\{\frac{8}{9}m+n=1}\end{array}\right.$,
解可得m=1,n=$\frac{1}{9}$,
故要求椭圆的标准方程为:$\frac{{x}^{2}}{1}$+$\frac{{y}^{2}}{9}$=1.
点评 本题考查椭圆的标准方程的求法,可以依据题意,设出椭圆的标准方程,然后用待定系数法进行求解.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案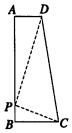 如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3.如果AB边上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,那么这样的点P有( )
如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3.如果AB边上的点P使得以P,A,D为顶点的三角形和以P,B,C为顶点的三角形相似,那么这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 2个 |
| A. | -$\frac{7\sqrt{2}}{10}$ | B. | -$\frac{\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
| A. | $\frac{{\sqrt{3}}}{8}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{3}}}{24}$ | D. | $\frac{{\sqrt{3}}}{48}$ |
 已知点($\sqrt{2}$,2)在幂函数f(x)的图象上,点(2,$\frac{1}{2}$)在幂函数g(x)的图象上.
已知点($\sqrt{2}$,2)在幂函数f(x)的图象上,点(2,$\frac{1}{2}$)在幂函数g(x)的图象上.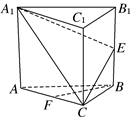 如图,在正三棱柱ABCA1B1C1中,E,F分别为BB1,AC的中点.求证:BF∥平面A1EC.
如图,在正三棱柱ABCA1B1C1中,E,F分别为BB1,AC的中点.求证:BF∥平面A1EC.