题目内容
17.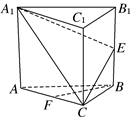 如图,在正三棱柱ABCA1B1C1中,E,F分别为BB1,AC的中点.求证:BF∥平面A1EC.
如图,在正三棱柱ABCA1B1C1中,E,F分别为BB1,AC的中点.求证:BF∥平面A1EC.
分析 以F为原点,FC为x轴,FB为y轴,过F作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能证明BF∥平面A1EC.
解答 证明:以F为原点,FC为x轴,FB为y轴,过F作平面ABC的垂线为z轴,
建立空间直角坐标系,
设AB=2,AA1=2t,则B(0,$\sqrt{3}$,0),F(0,0,0),
A1(-1,0,2t),C(1,0,0),E(0,$\sqrt{3}$,t),
$\overrightarrow{FB}$=(0,$\sqrt{3}$,0),$\overrightarrow{C{A}_{1}}$=(-2,0,2t),$\overrightarrow{CE}$=(-1,$\sqrt{3},t$),
设平面A1EC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{C{A}_{1}}=-2x+2tz=0}\\{\overrightarrow{n}•\overrightarrow{CE}=-x+\sqrt{3}y+tz=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(t,0,1),
∵$\overrightarrow{FB}•\overrightarrow{n}$=0,且BF?平面A1EC,
∴BF∥平面A1EC.
点评 本题考查线面平行的证明,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.某公司发布的2015年度财务报告显示,该公司在去年第一季度、第二季度的营业额每季度均比上季度下跌10%,第三季度、第四季度的营业额每季度均比上季度上涨10%,则该公司在去年整年的营业额变化情况是( )
| A. | 下跌1.99% | B. | 上涨1.99% | C. | 不涨也不跌 | D. | 不确定 |
2.在等差数列{an}中,若ap=4,aq=2且p=4+q,则公差d=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | -1 |
9.若函数f(x)为偶函数,且在[0,+∞)上是增函数,又f(-3)=0,则不等式(x-2)f(x)<0的解集为( )
| A. | (-2,3) | B. | (-3,-2)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(2,3) |
6.设a=30.4,b=log40.3,c=log43,则( )
| A. | a>c>b | B. | b>c>a | C. | c>a>b | D. | c>b>a |
7.“-3≤m≤0”是“直线mx-y-2m=0与函数$f(x)=\left\{\begin{array}{l}\sqrt{-{x^2}+16},-4≤x≤0\\ 2x-2,x>0\end{array}\right.$的图象有两个交点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |