题目内容
经过A(6,5),B(0,1)两点,并且圆心在直线3x+10y+9=0上的圆方程为 .
考点:圆的标准方程
专题:直线与圆
分析:设出圆心坐标,利用待定系数法即可得到结论.
解答:
解:∵圆心在直线3x+10y+9=0,
∴设所求的圆的圆心为C(a,
),
则|CA|=|CB|,即(a-6)2+(
-5)2=a2+(
-1)2,
解得:a=7,
∴圆心C(7,-3),半径r=|CB|=
=
,
则所求圆的方程为(x-7)2+(y+3)2=65.
故答案为:(x-7)2+(y+3)2=65
∴设所求的圆的圆心为C(a,
| -3a-9 |
| 10 |
则|CA|=|CB|,即(a-6)2+(
| -3a-9 |
| 10 |
| -3a-9 |
| 10 |
解得:a=7,
∴圆心C(7,-3),半径r=|CB|=
| 72+42 |
| 65 |
则所求圆的方程为(x-7)2+(y+3)2=65.
故答案为:(x-7)2+(y+3)2=65
点评:本题主要考查圆的标准方程的求解,根据条件设出圆心,利用两点间的距离公式是解决本题的关键.考查学生计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某产品的广告费用x与销售额y的统计数据如表:
根据上表利用最小二乘法可得回归方程
=
x+
,据此模型预报广告费用为7万元时销售额为74.9万元,则据此模型预报,广告费每增加1万元,销售额大约增加( )
| x | 2 | 3 | 4 | 5 |
| y | 26 | 39 | 49 | 54 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
| A、9.1万元 | B、9.4万元 |
| C、9.7万元 | D、10万元 |
已知集合A={x|x(x-1)≤0,x∈R},B={x|-2<x<1,x∈R},那么集合A∩B是( )
| A、{x|-2<x≤1,x∈R} |
| B、{x|0≤x<1,x∈R} |
| C、{x|0<x≤1,x∈R} |
| D、{x|0<x<1,x∈R} |
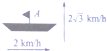 如图,一艘船从A点出发以2
如图,一艘船从A点出发以2 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+