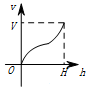圆心角为2弧度的扇形的周长为3.则此扇形的面积为$\frac{9}{16}$．题目和参考答案——青夏教育精英家教网—

题目内容

13．圆心角为2弧度的扇形的周长为3，则此扇形的面积为$\frac{9}{16}$．

分析根据扇形的周长求出半径r，再根据扇形的面积公式计算即可．

解答解：设该扇形的半径为r，
根据题意，有l=αr+2r，
∴3=2r+2r，
∴r=$\frac{3}{4}$，
∴S_扇形=$\frac{1}{2}$αr²=$\frac{1}{2}$×2×$\frac{9}{16}$=$\frac{9}{16}$．
故答案为：$\frac{9}{16}$．

点评本题考查了弧度制下扇形的面积及弧长公式的运用问题，是基础题目．

练习册系列答案

4．$tanϕ=-\sqrt{3}$，ϕ为第四象限角，则cosϕ=（　　）

$\frac{{\sqrt{3}}}{2}$

D．

-$\frac{{\sqrt{3}}}{2}$

1．函数$y=\sqrt{{{log}_{\frac{1}{2}}}{x^2}}$的单调递增区间是[-1，0）．

8．对于原命题：“已知a，b，c∈R，若a＞b，则ac²＞bc²”，以及它的逆命题、否命题、逆否命题，在这4个命题中，真命题的个数为（　　）

18．已知函数f（x）=ax²+2ax+4（-3＜a＜0），其图象上两点的横坐标为x₁、x&₂满足x₁＜x₂，且x₁+x₂=1+a，则由（　　）

	A．	f（x₁）＜f（x₂）		B．	f（x₁）=f（x₂）
	C．	f（x₁）＞f（x₂）		D．	f（x₁）、f（x&₂）的大小不确定

5．已知函数f（x）=x²-9，$g（x）=\frac{x}{x-3}$，那么f（x）•g（x）=x^2₊3x （x≠3）．

2．

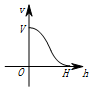
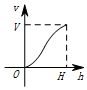
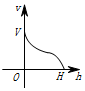
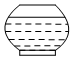一个高为H，容积为V的鱼缸的轴截面如图所示，向鱼缸里注水，若鱼缸里的水面高度为h时，鱼缸里的水的体积为V'，则函数V'=f（h）的大致图象可能是（　　）

3．设i是虚数单位，则复数z=i（3-4i）的虚部与模的和（　　）

试题分类