题目内容
已知函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:
①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立
②当x∈(0,5)时,x≤f(x)≤2|x-1|+1 恒成立
(1)求f(1)的.
(2)求f(x)的解析式
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f(x+t)≤x.
①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立
②当x∈(0,5)时,x≤f(x)≤2|x-1|+1 恒成立
(1)求f(1)的.
(2)求f(x)的解析式
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f(x+t)≤x.
考点:函数的最值及其几何意义
专题:计算题,综合题,函数的性质及应用
分析:(1)令x=1可得1≤f(1)≤2|1-1|+1;从而解得;
(2)结合当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立及二次函数的性质可求出二次函数的解析式;
(3)由二次函数的性质知,设g(x)=x2+(2t-2)x+t2+2t+1,则恒成立问题可化为g(1)=t2+4t≤0,g(m)=m2+(2t-2)m+t2+2t+1≤0;从而解得.
(2)结合当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立及二次函数的性质可求出二次函数的解析式;
(3)由二次函数的性质知,设g(x)=x2+(2t-2)x+t2+2t+1,则恒成立问题可化为g(1)=t2+4t≤0,g(m)=m2+(2t-2)m+t2+2t+1≤0;从而解得.
解答:
解:(1)∵当x∈(0,5)时,x≤f(x)≤2|x-1|+1 恒成立,
∴当x=1时,1≤f(1)≤2|1-1|+1;
∴f(1)=1;
(2)∵f(x-1)=f(-x-1),
∴函数f(x)=ax2+bx+c的图象关于x=-1对称,
又∵当x∈R时,f(x)的最小值为0,
∴f(x)=a(x+1)2,a>0;
又∵f(1)=4a=1;
∴a=
;
故f(x)=
(x+1)2;
(3)∵f(x+t)=
(x+t+1)2≤x,
∴x2+(2t-2)x+t2+2t+1≤0;
设g(x)=x2+(2t-2)x+t2+2t+1,
则g(1)=t2+4t≤0,g(m)=m2+(2t-2)m+t2+2t+1≤0;
则-4≤t≤0,1-t-2
≤m≤1-t+2
,
所以m≤1+4+2•
=9,
故m的最大值为9.
∴当x=1时,1≤f(1)≤2|1-1|+1;
∴f(1)=1;
(2)∵f(x-1)=f(-x-1),
∴函数f(x)=ax2+bx+c的图象关于x=-1对称,
又∵当x∈R时,f(x)的最小值为0,
∴f(x)=a(x+1)2,a>0;
又∵f(1)=4a=1;
∴a=
| 1 |
| 4 |
故f(x)=
| 1 |
| 4 |
(3)∵f(x+t)=
| 1 |
| 4 |
∴x2+(2t-2)x+t2+2t+1≤0;
设g(x)=x2+(2t-2)x+t2+2t+1,
则g(1)=t2+4t≤0,g(m)=m2+(2t-2)m+t2+2t+1≤0;
则-4≤t≤0,1-t-2
| -t |
| -t |
所以m≤1+4+2•
| 4 |
故m的最大值为9.
点评:本题考查了二次函数的性质及应用,同时考查了恒成立问题及存在性问题的应用,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
设集合M={x|y2=3x,x∈R},N={y|x2+y2=4,x∈R,y∈R},则M∩N等于( )
| A、[-2,2] | ||||
| B、[-2,2] | ||||
C、{(1,
| ||||
| D、[0,2] |
在平行四边形ABCD中,
=3
,AE的延长线与CD交于点F,若
=
,
=
,则
=( )
| BD |
| ED |
| AC |
| a |
| BD |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
从高h米的小岛看正东方向有一只船俯角为30°,看正南方向有一只船俯角为45°,则此时两船间的距离为( )
| A、2h米 | ||
B、
| ||
C、
| ||
D、2
|
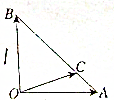 如图所示,在等腰Rt△AOB中,OA=OB=1,
如图所示,在等腰Rt△AOB中,OA=OB=1,