题目内容
已知向量
=(cosx,sin
),
=(0,cos
),x∈R,若函数f(x)=2+sinx-|a-b|2,且函数g(x)的图象与函数f(x)的图象关于原点成中心对称.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-λf(x)+1在x∈[-
,
]上是增函数,求实数λ的取值范围.
| a |
| x |
| 2 |
| b |
| x |
| 2 |
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)若h(x)=g(x)-λf(x)+1在x∈[-
| π |
| 2 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,平面向量数量积的坐标表示、模、夹角
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)首先根据向量的坐标运算求出向量的坐标和向量的模,进一步求出f(x)的关系式及g(x)的关系式.
(Ⅱ)利用上步的结论,进一步利用三角函数的导数与函数的单调性的关系,利用恒成立问题求出参数的范围.
(Ⅱ)利用上步的结论,进一步利用三角函数的导数与函数的单调性的关系,利用恒成立问题求出参数的范围.
解答:
解:(Ⅰ)向量
=(cosx,sin
),
=(0,cos
),则:
-
=(cosx,sin
-cos
)
|
-
|=|
-
|2=cos2x+1-sinx
则:f(x)=2+sinx-|a-b|2
=2+2sinx-cos2x
=sin2x+2sinx
由于函数g(x)的图象与函数f(x)的图象关于原点成中心对称.
所以:g(x)=-f(-x)=-sin2x+2sinx
(Ⅱ)由(Ⅰ)得:h(x)=g(x)-λf(x)+1
=-sin2x+2sinx-λsin2x-2λsinx+1
=-(1+λ)sin2x+2(1-λ)sinx+1sin2x+2(1-λ)sinx+1
所以:h′(x)=-(1+λ)2sinxcosx+2(1-λ)cosx
=2cosx[-(1+λ)sinx+1-λ]
由于x∈[-
,
]函数h(x)是增函数.
所以h′(x)≥0
又由于cosx≥0
故只需[-(1+λ)sinx+1-λ]>0即可.
则:λ<
=
-1
则λ≤(
-1)min即可
由于x∈[-
,
]时,(
-1)min≥0
所以:λ≤0
| a |
| x |
| 2 |
| b |
| x |
| 2 |
| a |
| b |
| x |
| 2 |
| x |
| 2 |
|
| a |
| b |
| a |
| b |
则:f(x)=2+sinx-|a-b|2
=2+2sinx-cos2x
=sin2x+2sinx
由于函数g(x)的图象与函数f(x)的图象关于原点成中心对称.
所以:g(x)=-f(-x)=-sin2x+2sinx
(Ⅱ)由(Ⅰ)得:h(x)=g(x)-λf(x)+1
=-sin2x+2sinx-λsin2x-2λsinx+1
=-(1+λ)sin2x+2(1-λ)sinx+1sin2x+2(1-λ)sinx+1
所以:h′(x)=-(1+λ)2sinxcosx+2(1-λ)cosx
=2cosx[-(1+λ)sinx+1-λ]
由于x∈[-
| π |
| 2 |
| π |
| 2 |
所以h′(x)≥0
又由于cosx≥0
故只需[-(1+λ)sinx+1-λ]>0即可.
则:λ<
| 1-sinx |
| 1+sinx |
| 2 |
| 1+sinx |
则λ≤(
| 2 |
| 1+sinx |
由于x∈[-
| π |
| 2 |
| π |
| 2 |
| 2 |
| 1+sinx |
所以:λ≤0
点评:本题考查的知识要点:向量的坐标运算,向量的模,函数图象的对称问题,三角函数的导数与单调性的关系恒成立问题的应用,属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若空间几何体的三视图如图所示,则该几何体体积为( )
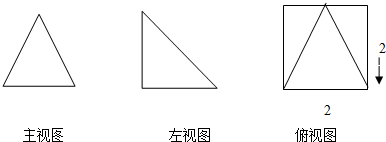

A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
点P为底边长为2
,高为2的正三棱柱表面上的动点,MN是该棱柱内切球的一条直径,则
•
取值范围是( )
| 3 |
| PM |
| PN |
| A、[0,2] |
| B、[0,3] |
| C、[0,4] |
| D、[-2,2] |
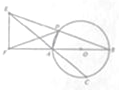 如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F.
如图所示,AB是⊙O的直径,弦BD、CA的延长线相交于点E,EF垂直BA并交BA的延长线于点F.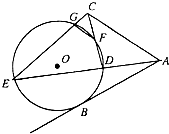 如图,AB是⊙O的一条切线,切点为B,直线ADE,CFD,CGE都是⊙O的割线,已知AC=AB.
如图,AB是⊙O的一条切线,切点为B,直线ADE,CFD,CGE都是⊙O的割线,已知AC=AB.