题目内容
设
=(-
,cosωx),
=(1,
cosωx-sinωx)(ω>0),f(x)=
•
,若f(x)的最小正周期是π.
(Ⅰ)求ω的值;
(Ⅱ)求f(x)在区间[
,
]上的值域.
| a |
| ||
| 2 |
| b |
| 3 |
| a |
| b |
(Ⅰ)求ω的值;
(Ⅱ)求f(x)在区间[
| π |
| 12 |
| 7π |
| 12 |
考点:三角函数中的恒等变换应用,平面向量数量积的坐标表示、模、夹角,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:(Ⅰ)首先利用向量的数量积对三角函数的关系式进行三角恒等变换,把三角函数变形成余弦型函数,进一步利用函数的周期求出函数的解析式.
(Ⅱ)直接利用上步的结论,利用函数的定义域求出函数的值域.
(Ⅱ)直接利用上步的结论,利用函数的定义域求出函数的值域.
解答:
解:(Ⅰ)已知:
=(-
,cosωx),
=(1,
cosωx-sinωx)(ω>0),
则:f(x)=
•
=
cos2ωx-sinωxcosωx-
=
-
-
=cos2ωxcos
-sin2ωxsin
=cos(2ωx+
)
若f(x)的最小正周期是π
所以:T=
=π
解得:ω=1
(Ⅱ)由(Ⅰ)得:f(x)=cos(2x+
)
由于:x∈[
,
]
所以:2x+
∈[
,
]
所以:函数f(x)的值域为:[-1,
]
| a |
| ||
| 2 |
| b |
| 3 |
则:f(x)=
| a |
| b |
| 3 |
| ||
| 2 |
=
| ||
| 2 |
| sin2ωx |
| 2 |
| ||
| 2 |
=cos2ωxcos
| π |
| 6 |
| π |
| 6 |
=cos(2ωx+
| π |
| 6 |
若f(x)的最小正周期是π
所以:T=
| 2π |
| 2ω |
解得:ω=1
(Ⅱ)由(Ⅰ)得:f(x)=cos(2x+
| π |
| 6 |
由于:x∈[
| π |
| 12 |
| 7π |
| 12 |
所以:2x+
| π |
| 6 |
| π |
| 3 |
| 4π |
| 3 |
所以:函数f(x)的值域为:[-1,
| 1 |
| 2 |
点评:本题考查的知识要点:利用向量的数量积对三角函数进行恒等变换,利用函数的周期求函数的解析式,利用函数的定义域求函数的值域.属于基础题型.

练习册系列答案
相关题目
已知某个几何体的三视图如图,则这个几何体的表面积为( )
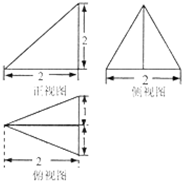

A、4+
| ||
B、4+2
| ||
| C、6 | ||
| D、8 |
等比数列{an}的前n项和为Sn,已知a1=2014,且an+2an+1+an+2=0(n∈N*),则S2014=( )
| A、2013 | B、2014 |
| C、1 | D、0 |
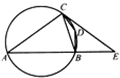 如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.
如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.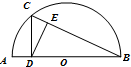 如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=
如图,在半圆O中,C是圆O上一点,直径AB⊥CD,垂足为D,DE⊥BC,垂足为E,若AB=6,AD=1,则CE•BC=