题目内容
18.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F2,M(x0,y0)(x0>0,y0>0)是双曲线C上的点,N(-x0,-y0),连接MF2并延长MF2交双曲线C于点P,连接NF2,PN,若△NF2P是以∠NF2P为顶角的等腰直角三角形,则双曲线C的渐近线方程为y=±$\frac{\sqrt{6}}{2}$x.分析 可设双曲线的左焦点为F1,并连接MF1,MF2,根据双曲线的对称性及条件便知四边形F1NF2M为矩形,可设MF2=x,并连接PF1,这样根据双曲线的定义及平行四边形对边相等即可得出MF1=2a+x,MP=2a+2x,PF1=4a+x,这样根据直角三角形的边的关系即可得到(2a+x)2+x2=4c2 ①;:(2a+x)2+(2a+2x)2=(4a+x)2 ②;这样可以由②解出x,带入①中便可得到a,b,c的关系,根据c2=a2+b2即可得出$\frac{b}{a}$的值,从而便得出渐近线方程.
解答 解:如图,设F1为双曲线左焦点,连接MF1,NF1,则: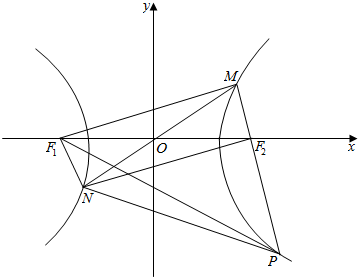
由对称性可知四边形F1NF2M
为平行四边形;
又△NF2P是以∠NF2P为顶角的等腰直角三角形,
可得∠MF2N=90°;
∴F1NF2M为矩形;
设|MF2|=x,由双曲线的定义可得,
|MF1|=2a+x;
∴|PF2|=|NF2|=|MF1|=2a+x;
∴|PF1|=2a+|PF2|=4a+x;
在Rt△MF1F2中有:
(2a+x)2+x2=4c2 ①;
在Rt△MF1P中有:(2a+x)2+(2a+2x)2=(4a+x)2 ②;
由②解得,x=a,代回①得:9a2+a2=4c2;
∴c2=$\frac{5}{2}$a2;
∴b2=c2-a2=$\frac{3}{2}$a2;
∴$\frac{b}{a}$=$\frac{\sqrt{6}}{2}$;
∴渐近线方程为:y=±$\frac{b}{a}$x=±$\frac{\sqrt{6}}{2}$x.
故答案为:y=±$\frac{\sqrt{6}}{2}$x.
点评 本题考查双曲线的对称性,双曲线的标准方程,双曲线的焦点,以及双曲线的定义,直角三角形的勾股定理,双曲线的渐近线方程,考查化简整理的运算能力,属于中档题.

 快捷英语周周练系列答案
快捷英语周周练系列答案| A. | y=x2 | B. | y=2x | C. | y=log2x | D. | y=2x |
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
| A. | 平行或异面 | B. | 异面 | C. | 相交 | D. | 以上都不对 |
| A. | $16\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $9(2+\sqrt{3})$ |
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 推理没有问题,结论正确 |