题目内容
7.已知△ABC中,AB=2,AC=4,点D是边BC的中点,则$\overrightarrow{BC}$•$\overrightarrow{AD}$等于6.分析 根据题意,利用平面向量的加、减法运算法则,表示出$\overrightarrow{BC}$与$\overrightarrow{AD}$,求出数量积即可.
解答 解:如图所示,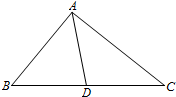
根据向量的加减法法则有:
$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,
$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{AB}$,
此时$\overrightarrow{BC}$•$\overrightarrow{AD}$=($\overrightarrow{AC}$-$\overrightarrow{AB}$)•($\frac{1}{2}$$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{AB}$)
=$\frac{1}{2}$${\overrightarrow{AC}}^{2}$-$\frac{1}{2}$${\overrightarrow{AB}}^{2}$
=$\frac{1}{2}$×42-$\frac{1}{2}$×22
=6.
故答案为:6.
点评 本题考查了平面向量的线性运算与数量积运算问题,是基础题目.

练习册系列答案
相关题目
17.已知数列{an}的前n项和为Sn,${a_n}={({-1})^{n-1}}(4n-3)$,则S11的值等于( )
| A. | 21 | B. | -21 | C. | 41 | D. | 61 |
15.角α的终边过点(3a-9,a+2),且cosα<0,sinα>0,则a的范围是( )
| A. | (-2,3) | B. | [-2,3) | C. | (-2,3] | D. | [-2,3] |
17.设全集U={0,1,2,3},集合A={0,2},集合B={2,3},则(∁UA)∪B=( )
| A. | {3} | B. | {2,3} | C. | {1,2,3} | D. | {0,1,2,3} |