题目内容
已知函数f（x）=
的图象为曲线C．
（1）求曲线C：y=f（x）在点A（1，0）处的切线l的方程．
（2）证明：除切点（1，0）之外，切线l在曲线C的上方．
| lnx |
| x |
（1）求曲线C：y=f（x）在点A（1，0）处的切线l的方程．
（2）证明：除切点（1，0）之外，切线l在曲线C的上方．
考点：利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题：综合题,导数的概念及应用
分析：（1）求出切点处切线斜率，代入点斜式方程，可以求解；
（2）设g(x)=x-1-
，利用导数分析函数的单调性，可得g（x）≥g（1）=0，从而可得结论．
（2）设g(x)=x-1-
| lnx |
| x |
解答：
（1）解：∵f（x）=
，
∴f′（x）=
，
∴f′（1）=1，
∴曲线C：y=f（x）在点A（1，0）处的切线l的方程为y=x-1；
（2）证明：设g(x)=x-1-
，可得g/(x)=
．
当x≥1时，g（x）为递增；当0＜x＜1时g（x）为递减，
∴g（x）≥g（1）=0，
∴x-1≥
，即除切点（1，0）之外，切线l在曲线C的上方．
| lnx |
| x |
∴f′（x）=
| 1-lnx |
| x2 |
∴f′（1）=1，
∴曲线C：y=f（x）在点A（1，0）处的切线l的方程为y=x-1；
（2）证明：设g(x)=x-1-
| lnx |
| x |
| x2-1+lnx |
| x2 |
当x≥1时，g（x）为递增；当0＜x＜1时g（x）为递减，
∴g（x）≥g（1）=0，
∴x-1≥
| lnx |
| x |
点评：本题考查的知识点是导数的几何意义，利用导数研究函数的单调性，是导数的综合应用，难度中档．
练习册系列答案
相关题目
函数f（x）=sinωx（ω＞0）的图象在y轴右边的第一条对称轴的方程x=1，则ω=（ ）
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
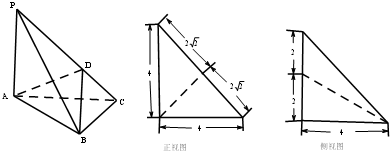
在三棱椎P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上的一点，它的正视图和侧视图如图所示，则下列命题正确的是（ ）
A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|
如图，△ABC的三个内角分别为A，B，C，cosA=