题目内容
已知双曲线
-
=1(a>0,b>0)的右焦点为F(c,0),直线x=
与一条渐近线交于点A,△OAF的面积为
(O为原点),则抛物线y2=
x的准线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| a2 |
| 2 |
| 4a |
| b |
| A、x=-1 | B、x=-2 |
| C、y=-1 | D、y=-2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线方程求得其渐近线方程,与直线方程联立求得点A的坐标,进而利用△OAF的面积求得a和b的关系式,带入抛物线方程,求得抛物线方程,最后利用抛物线的性质求得准线方程.
解答:
解:依题意知,双曲线渐近线方程为:y=±
,
根据对称性可知,A点在x轴上方和下方的解是一样的,
故看A在x轴上方时,联立方程,
,求得y=
∴S△OAF=
•C•
=
,
∴a=b,
∴抛物线的方程为y2=4x,
即2p=4,p=2
∴抛物线的准线方程为x=-1,
故选:A.
| b |
| a |
根据对称性可知,A点在x轴上方和下方的解是一样的,
故看A在x轴上方时,联立方程,
|
| ab |
| c |
∴S△OAF=
| 1 |
| 2 |
| ab |
| c |
| a2 |
| 2 |
∴a=b,
∴抛物线的方程为y2=4x,
即2p=4,p=2
∴抛物线的准线方程为x=-1,
故选:A.
点评:本题主要考查了抛物线和双曲线的基本性质.解题的关键是求得a和b的关系.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn(n∈N*),且an=2n+λ,若数列{Sn}为递增数列,则实数λ的取值范围为( )
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-4,+∞) |
| D、[-4,+∞) |
函数f(x)=sinωx(ω>0)的图象在y轴右边的第一条对称轴的方程x=1,则ω=( )
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
在复平面内,复数
-i3对应的点位于( )
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( )
已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( )A、18
| ||
B、36
| ||
C、45
| ||
D、54
|
已知函数f(x)=ax2+bx+c(a,b,c∈R,a<0)对于一切实数x都有f(1-x)=f(1+x),而且f(-1)<0,f(0)>0,则有( )
| A、a+b+c<0 |
| B、c<2b |
| C、abc>0 |
| D、b<a+c |
在三棱椎P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上的一点,它的正视图和侧视图如图所示,则下列命题正确的是( )
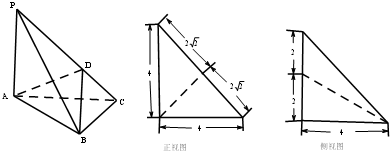

A、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
B、BD⊥平面PAC且三棱椎D-ABC的体积为
| ||
C、AD⊥平面PBC且三棱椎D-ABC的体积为
| ||
D、BD⊥平面PAC且三棱椎D-ABC的体积为
|
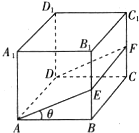 如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,
如图正方体ABCD-A1B1C1D1的棱长为1,点E在线段BB1和线段A1B1上移动,∠EAB=θ,θ∈(0,