题目内容
2.函数y=$\frac{{2}^{x}}{{2}^{x}+1}$(x>0)的值域是($\frac{1}{2}$,1).分析 由题意可得t=2x+1>2,换元由不等式的性质可得.
解答 解:∵x>0,∴t=2x+1>2,
∴y=$\frac{{2}^{x}}{{2}^{x}+1}$=$\frac{t-1}{t}$=1-$\frac{1}{t}$,
由t>2可得0<$\frac{1}{t}$<$\frac{1}{2}$,
∴-$\frac{1}{2}$<-$\frac{1}{t}$<0,∴$\frac{1}{2}$<1-$\frac{1}{t}$<1
故答案为:($\frac{1}{2}$,1)
点评 本题考查函数的值域,换元并利用不等式的性质是解决问题的关键,属基础题.

练习册系列答案
相关题目
10.直线l垂直于直线y=x+1,原点O到l的距离为1,且l与y轴正半轴有交点,则直线l的方程是( )
| A. | x+y-$\sqrt{2}$=0 | B. | x+y+1=0 | C. | x+y-1=0 | D. | x+y+$\sqrt{2}$=0 |
7.设a∈R,则1+a+a2+…+an的值为( )
| A. | $\frac{1-{a}^{n}}{1-a}$ | B. | $\frac{1-{a}^{n+1}}{1-a}$ | C. | $\frac{1-{a}^{n+1}}{1-a}$或n+1 | D. | 以上都不是 |
14.设点P为有公共焦点F1、F2的椭圆M和双曲线Г的一个交点,且cos∠F1PF2=$\frac{3}{5}$,椭圆M的离心率为e1,双曲线Г的离心率为e2.若e2=2e1,则e1=( )
| A. | $\frac{\sqrt{7}}{5}$ | B. | $\frac{\sqrt{7}}{4}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{10}}{4}$ |
14.如图为一几何体的三视图,其中这三个视图完全一样,则该几何体的表面积为( )
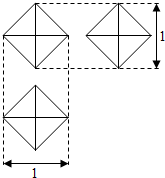

| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 6 |
15.已知椭圆$\frac{x^2}{2}$+y2=1与直线y=x+m交于A、B两点,且|AB|=$\frac{4\sqrt{2}}{3}$,则实数m的值为( )
| A. | ±1 | B. | ±$\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | ±$\sqrt{2}$ |