题目内容
7.已知$\root{3}{2+\frac{2}{7}}$=2$\root{3}{\frac{2}{7}}$,$\root{3}{3+\frac{3}{26}}$=3$\root{3}{\frac{3}{26}}$,$\root{3}{4+\frac{4}{63}}$=4$\root{3}{\frac{4}{63}}$,…,$\root{3}{2014+\frac{m}{n}}$=2014$\root{3}{\frac{m}{n}}$,$…\root{3}{{2016+\frac{a}{b}}}=2016\root{3}{{\frac{a}{b}}}$,则$\frac{b+1}{a^2}$=2016.分析 观察易知:a=2016,20163-1=b,所以b+1=20163,即可得出结论.
解答 解:观察易知:a=2016,20163-1=b,所以b+1=20163,
故$\frac{b+1}{a^2}=\frac{{{{2016}^3}}}{{{{2016}^2}}}=2016$.
故答案为2016.
点评 本题考查归纳推理,考查学生的计算能力,正确发现规律是关键.

练习册系列答案
相关题目
15.下面命题:
①如果让实数a与ai对应,那么实数集与纯虚数集一一对应;
②两个复数互为共轭复数的充要条件是其积为实数;
③x=y=1是x+yi=1+i的充分非必要条件;
④0比-i大.
其中正确的命题的个数是( )
①如果让实数a与ai对应,那么实数集与纯虚数集一一对应;
②两个复数互为共轭复数的充要条件是其积为实数;
③x=y=1是x+yi=1+i的充分非必要条件;
④0比-i大.
其中正确的命题的个数是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
2.在同一平面直角坐标系中,点A($\frac{1}{3}$,-2)经过伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$所得的点A′的坐标为( )
| A. | (1,-1) | B. | (1,-4) | C. | $({\frac{1}{9},-4})$ | D. | (9,-1) |
12.设集合A={x|x≥-1},B={x|y=ln(x-2},则A∩∁RB=( )
| A. | [-1,2) | B. | [2,+∞) | C. | [-1,2] | D. | [-1,+∞) |
19.某空间几何体的三视图如图所示,则该几何体的体积是( )


| A. | 32 | B. | 32$\sqrt{2}$ | C. | $\frac{32}{3}$ | D. | $\frac{32}{3}$$\sqrt{2}$ |
16.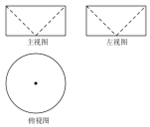 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的表面积为( )| A. | ($\sqrt{2}$+1)π | B. | ($\sqrt{2}$+2)π | C. | ($\sqrt{2}$+3)π | D. | ($\sqrt{2}$+4)π |