题目内容
2.在同一平面直角坐标系中,点A($\frac{1}{3}$,-2)经过伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$所得的点A′的坐标为( )| A. | (1,-1) | B. | (1,-4) | C. | $({\frac{1}{9},-4})$ | D. | (9,-1) |
分析 由伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$得到$\left\{\begin{array}{l}{x′=3x}\\{y′=\frac{1}{2}y}\end{array}\right.$,即可得出结论.
解答 解:设点A′(x′,y′).
由伸缩变换φ:$\left\{\begin{array}{l}{x′=3x}\\{2y′=y}\end{array}\right.$得到$\left\{\begin{array}{l}{x′=3x}\\{y′=\frac{1}{2}y}\end{array}\right.$,
又已知点A($\frac{1}{3}$,-2).
于是x′=1,y′=-1,
∴变换后点A′的坐标为(1,-1).
故选A.
点评 本题考查了坐标变换,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
13.经过点M(m,3)和N(1,m)的直线l与斜率为-1的直线互相垂直,则m的值是( )
| A. | 4 | B. | 1 | C. | 2 | D. | 3 |
10.命题p:在△ABC中,∠C>∠B是sinC>sinB的充要条件;命题q:a>b是ac2>bc2的充分不必要条件,则( )
| A. | “p∨q”为假 | B. | “p∧q”为真 | C. | ¬p为假 | D. | ¬q为假 |
17.已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得,在y2=2px两边同时对x求导,得2yy'=2p,则$y'=\frac{p}{y}$,所以过点P的切线的斜率$k=\frac{p}{y_0}$,试用上述方法求出双曲线${x^2}-\frac{y^2}{2}=1$在$P({\sqrt{2},\sqrt{2}})$处的切线方程为( )
| A. | 2x-y=0 | B. | $2x-y-\sqrt{2}=0$ | C. | $2x-3y-\sqrt{2}=0$ | D. | $x-y-\sqrt{2}=0$ |
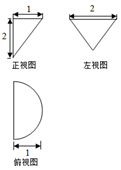
14.一几何体的三视图如图所示,则它的体积为( )


| A. | $\frac{{5\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |