Question

如图，正方形ABCD所在平面与直角三角形ABE所在的平面互相垂直，AE⊥AB，设M，N分别是DE，AB的中点，已知AB=2，AE=1
（Ⅰ）求证：MN∥平面BEC；
（Ⅱ）求点E到平面BMC的距离．

Answer 1

考点：直线与平面平行的判定,点、线、面间的距离计算

专题：计算题,作图题,证明题,空间位置关系与距离

分析：（Ⅰ）取EC中点F，连接MF，BF．由线线平行证明线面平行，（Ⅱ）将体积等价转化，求出体积，再求出底面面积，从而求高，得距离．

解答： 解：（Ⅰ）证明：取EC中点F，连接MF，BF．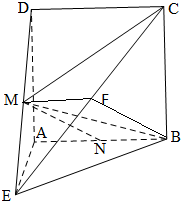
∵MF为△CDE的中位线，
∴MF∥CD，MF=

1

2

CD；
又∵NB∥CD，NB=

1

2

CD，
∴NB∥MF，NB=MF
∴四边形NBFM为平行四边形，
∴MN∥BF，又∵BF⊆平面BEC，MN?平面BEC，
∴MN∥平面BEC；
（Ⅱ）∵MN∥平面BEC，
∴VE-BMC=VM-BEC=VN-BEC=VC-BEN=

1

3

S△BEN•CB=

1

3

×

1

2

×2=

1

3

∵AB⊥AD，AB⊥AE，
∴AB⊥平面EAD，
∴AB⊥AM，
则MB=

MA2+AB2

=

( 1 2 DE)2+AB2

=

( 5 2 )2+22

=

21

2

∵CD∥AB，
∴CD⊥平面EAD，故CD⊥DM，
则MC=

MD2+DC2

=

( 1 2 DE)2+DC2

=

( 5 2 )2+22

=

21

2

在△BMC中，MB=MC=

21

2

，BC=2，
∴S△BMC=

1

2

•BC•

MB2-( 1 2 BC)2

=

1

2

×2×

21 4 -1

=

17

2

∴VE-BMC=

1

3

S△BMC•h=

1

3

（其中h表示点E到平面BMC的距离），
即

1

3

×

17

2

×h=

1

3

，
解得，h=

2 17

17

，
即点E到平面BMC的距离为

2

17

17

．

点评：本题综合考查了空间中线面的位置关系及距离问题，属于中档题．