题目内容
已知函数y=lgcos(2x),
(1)求函数的定义域、值域;
(2)讨论函数的奇偶性;
(3)讨论函数的周期性
(4)讨论函数的单调性.
(1)求函数的定义域、值域;
(2)讨论函数的奇偶性;
(3)讨论函数的周期性
(4)讨论函数的单调性.
考点:对数函数图象与性质的综合应用
专题:计算题,函数的性质及应用
分析:讨论f(x)=cos2x的性质,即可求得结论.
解答:
解:(1)由cos(2x)>0,可得函数的定义域(-
+kπ,
+kπ)(k∈Z),
∵0<cos(2x)≤1,∴函数的值域(-∞,0]…(3分)
(2)∵lgcos(-2x)=lgcos(2x),∴函数是偶函数…(5分)
(3)T=π…(8分)
(4)f(x)=cos2x的增区间为(-
+kπ,kπ)(k∈Z),减区间(kπ,kπ+
)(k∈Z),
∴函数y=lgcos(2x)的增区间为(-
+kπ,kπ)(k∈Z),减区间(kπ,kπ+
)(k∈Z)…(10分)
| π |
| 4 |
| π |
| 4 |
∵0<cos(2x)≤1,∴函数的值域(-∞,0]…(3分)
(2)∵lgcos(-2x)=lgcos(2x),∴函数是偶函数…(5分)
(3)T=π…(8分)
(4)f(x)=cos2x的增区间为(-
| π |
| 4 |
| π |
| 4 |
∴函数y=lgcos(2x)的增区间为(-
| π |
| 4 |
| π |
| 4 |
点评:本题考查对数函数图象与性质的综合应用,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
从3名男生和2名女生中选出3名代表去参加辩论比赛,则所选出的3名代表中至少有1名女生的选法共有( )
| A、9种 | B、10种 |
| C、12种 | D、20种 |
从点P(1,-2)引圆(x+1)2+(y-1)2=4的切线,则切线长是( )
| A、4 | B、3 | C、2 | D、1 |
 如图,正方形ABCD所在平面与直角三角形ABE所在的平面互相垂直,AE⊥AB,设M,N分别是DE,AB的中点,已知AB=2,AE=1
如图,正方形ABCD所在平面与直角三角形ABE所在的平面互相垂直,AE⊥AB,设M,N分别是DE,AB的中点,已知AB=2,AE=1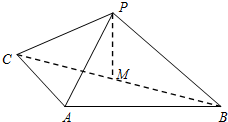 如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.
如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.