题目内容
已知函数f(x)=x+
(a<0),g(x)=2lnx+bx,且函数g(x)在x=1处的切线斜率为2.
(1)若对[1,+∞)内的一切实数x,不等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=-1时,求最大的正整数k,使得对[e,3]内的任意k个实数x1、x2、…xk都有f(x1)+f(x2)+…+f(xk)≤16g(xk)成立;
(3)求证:ln(2n+1)<
+
(n∈N*).
| a |
| x |
(1)若对[1,+∞)内的一切实数x,不等式f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=-1时,求最大的正整数k,使得对[e,3]内的任意k个实数x1、x2、…xk都有f(x1)+f(x2)+…+f(xk)≤16g(xk)成立;
(3)求证:ln(2n+1)<
| n |
| 2 |
| n |
 |
| i=1 |
| 6i+1 |
| 4i2-1 |
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:计算题,证明题,导数的综合应用,不等式的解法及应用
分析:(1)求出g(x)的导数,由导数的几何意义,即可求得,b=0,若对[1,+∞)内的一切实数x,不等式f(x)≥g(x)恒成立,转化为-a≤x2-2xlnx恒成立,利用导数即可求实数a的取值范围;
(2)求出f(x)的导数,求得f(x)在[e,3]上的最大值,要对[e,3]内的任意k个实数x1,x2,…,xk都有f(x1)+f(x2)+…+f(xk-1)≤16g(xk)成立,必须使得不等式左边的最大值小于或等于右边的最小值,得到不等式(k-1)×
≤16×2,解得即可;
(3)由(1)知,当x>1时,lnx<
(x-
)成立.不妨令x=
,x∈N*,先证明
[ln(2k+1)-ln(2k-1)]<
,再代入累加,即可得出ln(2n+1)<
<
+
(n∈N*),即可得证.
(2)求出f(x)的导数,求得f(x)在[e,3]上的最大值,要对[e,3]内的任意k个实数x1,x2,…,xk都有f(x1)+f(x2)+…+f(xk-1)≤16g(xk)成立,必须使得不等式左边的最大值小于或等于右边的最小值,得到不等式(k-1)×
| 8 |
| 3 |
(3)由(1)知,当x>1时,lnx<
| 1 |
| 2 |
| 1 |
| x |
| 2k+1 |
| 2k-1 |
| 1 |
| 4 |
| k |
| 4k2-1 |
| n |
 |
| i=1 |
| 4i |
| 4i2-1 |
| n |
| 2 |
| n |
 |
| i=1 |
| 6i+1 |
| 4i2-1 |
解答:
解:(1)g(x)=2lnx+bx的导数g′(x)=
+b,
由于函数g(x)在x=1处的切线斜率为2,
即有2+b=2,解得,b=0,即有g(x)=2lnx.
由f(x)≥g(x)整理,得
≤x-2lnx,
由于x≥1,要使不等式f(x)≥g(x)恒成立,
必须-a≤x2-2xlnx恒成立.
设h(x)=x2-2xlnx,h′(x)=2x-2lnx-2,
∵h″(x)=2-
,∴当x≥1时,h″(x)≥0,则h′(x)是增函数,
∴h′(x)≥h′(1)=0,h(x)是增函数,h(x)≥h(1)=0,-a≤1.
因此,实数a的取值范围是-1≤a<0.
(2)当a=-1时,f(x)=x-
,
∵f′(x)=1+
,
∴f(x)在[e,3](上是增函数,f(x)在[e,3]上的最大值为f(3)=
.
要对[e,3]内的任意k个实数x1,x2,…,xk都有f(x1)+f(x2)+…+f(xk-1)≤16g(xk)
成立,必须使得不等式左边的最大值小于或等于右边的最小值,
∵当x1=x2=…=xk-1=3时,不等式左边取得最大值,xk=e时不等式右边取得最小值.
∴(k-1)×
≤16×2,解得k≤13.
因此,k的最大值为13.
(3)证明:由(1)知,当x>1时,lnx<
(x-
)成立.
不妨令x=
,x∈N*,
∴ln
<
(
-
)=
,
∴
[ln(2k+1)-ln(2k-1)]<
,
∴
(ln3-ln1)<
,
(ln5-ln3)<
,
…,
[ln(2n+1)-ln(2n-1)<
,
累加可得
ln(2n+1)<
,
即有ln(2n+1)<4
=
<
+
(n∈N*).
则原不等式成立.
| 2 |
| x |
由于函数g(x)在x=1处的切线斜率为2,
即有2+b=2,解得,b=0,即有g(x)=2lnx.
由f(x)≥g(x)整理,得
| -a |
| x |
由于x≥1,要使不等式f(x)≥g(x)恒成立,
必须-a≤x2-2xlnx恒成立.
设h(x)=x2-2xlnx,h′(x)=2x-2lnx-2,
∵h″(x)=2-
| 2 |
| x |
∴h′(x)≥h′(1)=0,h(x)是增函数,h(x)≥h(1)=0,-a≤1.
因此,实数a的取值范围是-1≤a<0.
(2)当a=-1时,f(x)=x-
| 1 |
| x |
∵f′(x)=1+
| 1 |
| x2 |
∴f(x)在[e,3](上是增函数,f(x)在[e,3]上的最大值为f(3)=
| 8 |
| 3 |
要对[e,3]内的任意k个实数x1,x2,…,xk都有f(x1)+f(x2)+…+f(xk-1)≤16g(xk)
成立,必须使得不等式左边的最大值小于或等于右边的最小值,
∵当x1=x2=…=xk-1=3时,不等式左边取得最大值,xk=e时不等式右边取得最小值.
∴(k-1)×
| 8 |
| 3 |
因此,k的最大值为13.
(3)证明:由(1)知,当x>1时,lnx<
| 1 |
| 2 |
| 1 |
| x |
不妨令x=
| 2k+1 |
| 2k-1 |
∴ln
| 2k+1 |
| 2k-1 |
| 1 |
| 2 |
| 2k+1 |
| 2k-1 |
| 2k-1 |
| 2k+1 |
| 4k |
| 4k2-1 |
∴
| 1 |
| 4 |
| k |
| 4k2-1 |
∴
| 1 |
| 4 |
| 1 |
| 4×12-1 |
| 1 |
| 4 |
| 2 |
| 4×22-1 |
…,
| 1 |
| 4 |
| n |
| 4n2-1 |
累加可得
| 1 |
| 4 |
| n |
 |
| i=1 |
| i |
| 4i2-1 |
即有ln(2n+1)<4
| n |
 |
| i=1 |
| i |
| 4i2-1 |
| n |
 |
| i=1 |
| 4i |
| 4i2-1 |
| n |
| 2 |
| n |
 |
| i=1 |
| 6i+1 |
| 4i2-1 |
则原不等式成立.
点评:本题主要考查不等式恒成立以及不等式的证明,利用参数分离法转化为参数恒成立问题,利用导数的应用是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,若|
+
|=|
-
|,AB=2,AC=1,E,F为BC边的三等分点,则
•
=( )
| AB |
| AC |
| AB |
| AC |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
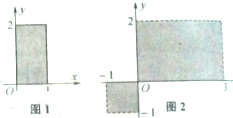 如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合:
如图,图1中以阴影部分(含边界)的点为元素所组成的集合用描述法表示为{(x,y)|0≤x≤1,0≤y≤2},则图2中以阴影部分(不含外边界但包含坐标轴)的点为元素所组成的集合: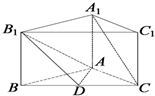 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,