题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线的斜率为
,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用双曲线的渐近线求出a、b关系,通过双曲线的几何量a、b、c的关系,求出双曲线的离心率.
解答:
解:由渐近线的斜率为
,可得
=
,即a=2b,故a2=4b2=4(a2-c2),故5a2=4c2,
故离心率为e=
=
.
故答案为:
.
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
故离心率为e=
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查双曲线的离心率的求法,双曲线的简单性质的应用.

练习册系列答案
相关题目
在△ABC中,若|
+
|=|
-
|,AB=2,AC=1,E,F为BC边的三等分点,则
•
=( )
| AB |
| AC |
| AB |
| AC |
| AE |
| AF |
A、
| ||
B、
| ||
C、
| ||
D、
|
已f(x)=2sin(
x+
),f(x)的最小正周期是( )
| π |
| 2 |
| π |
| 3 |
| A、2 | B、4π | C、2π | D、4 |
函数f(x)=x3+g(x)+1,其中g(x)(x∈R)为奇函数,若f(a)=2,则f(-a)的值为( )
| A、-2 | B、-1 | C、0 | D、3 |
不等式x+y-2<0表示的平面区域在直线x+y-2=0的( )
| A、右上方 | B、左上方 |
| C、右下方 | D、左下方 |
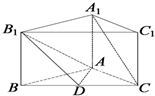 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,